题目内容
若椭圆C: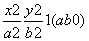 的离心率e为
的离心率e为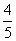 ,且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.
,且椭圆C的一个焦点与抛物线y2=-12x的焦点重合.
(1)求椭圆C的方程;
(2)设点M(2,0),点Q是椭圆上一点,当|MQ|最小时,试求点Q的坐标;
(3)设P(m,0)为椭圆C长轴(含端点)上的一个动点,过P点斜率为k的直线l交椭圆与A,B两点,若|PA|2+|PB|2的值仅依赖于k而与m无关,求k的值.
解:(1)∵·················∴椭圆C的方程为: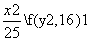 (2)设Q(x,y),-5≤x≤5
(2)设Q(x,y),-5≤x≤5
∴|MQ|2=(x-2)2+y2=x2-4x+4+16-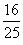 x2=
x2=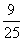 x2-4x+20
x2-4x+20
∵对称轴x=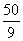 >5∴当x=5时,|MQ|2达到最小值,
>5∴当x=5时,|MQ|2达到最小值,
∴当|MQ|最小时,Q的坐标为(5,0) (3)设A(x1,y1),B(x2,y2),P(m,0)(-5≤m≤5),直线l:y=k(x-m)
由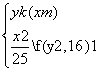 得x1+x2=
得x1+x2=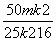 ,x1x2=-
,x1x2=-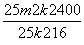 , ························8¢
, ························8¢
∴y1+y2=k(x1-m)+k(x2-m)=k(x1+x2)-2km=-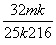
y1y2=k2(x1-m)(x2-m)=k2x1x2-k2m(x1+x2)+k2m2=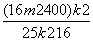
∴|PA|2+|PB|2=(x1-m)2+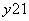 +(x2-m)2+
+(x2-m)2+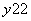
=(x1+x2)2-2x1x2-2a(x1+x2)+(y1+y2)2-2y1y2-2y1y2+2a2
=(k2+1)·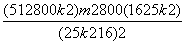
∵|PA|2+|PB|2的值仅依赖于k而与m无关
∴512-800k2=0∴k=±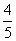 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,分别求
,分别求 ,
, ,
, ,然后归纳猜想一般性结论
,然后归纳猜想一般性结论 .
.
 、
、 为非零向量,则“
为非零向量,则“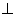
 为一次函数”的
为一次函数”的 、
、 ,满足
,满足 ,则
,则 的取值范围是
的取值范围是  ,
,  ,
, ,则
,则 等于( )
等于( )


 B.
B.


 ,若
,若 ,则实数a=________.
,则实数a=________. (
( >
> )的焦点为
)的焦点为 ,已知点
,已知点 ,
, 为抛物线上的两个动点,
为抛物线上的两个动点, .过弦
.过弦 的中点
的中点 作抛物线准线的垂线
作抛物线准线的垂线 ,垂足为
,垂足为 ,则
,则 的最大值为
的最大值为 B. 1 C.
B. 1 C.  D. 2
D. 2 与圆
与圆 的位置关系是
的位置关系是