题目内容
直线 R
R 与圆
与圆 的交点个数是( )
的交点个数是( )
| A.0 | B.1 | C.2 | D.无数个 |
C
解析试题分析:判断直线与圆的位置关系经常利用圆的几何性质来解决,即当圆心到直线的距离小于半径时,直线与圆相交,故本题应先求圆心(2,0)到直线x+ay-1=0的距离,再证明此距离小于半径,即可判断交点个数。解:圆 的圆心O(2,0),半径为2,圆心O到直线
的圆心O(2,0),半径为2,圆心O到直线 R
R 的距离为d=
的距离为d=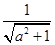 ∴a2+1≥1,∴d≤1<2,即圆心到直线的距离小于半径,,∴直线
∴a2+1≥1,∴d≤1<2,即圆心到直线的距离小于半径,,∴直线 R
R 与圆
与圆 的交点个数是2,故选C
的交点个数是2,故选C
考点:直线与圆的位置关系
点评:解决的关键是利用圆心到直线的距离与圆的半径的大小关系判定,属于基础题。

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
若直线 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )
A. | B. | C. | D. 或 或 |
已知圆 ,若过圆内一点
,若过圆内一点 的最长弦为
的最长弦为 ,最短弦为
,最短弦为 ;则四边形
;则四边形 的面积为( )
的面积为( )
A. | B. | C. | D. |
圆:x²+y²-4x+6y=0和圆:x²+y²-6x=0交于A,B两点,则AB的垂直平分线的方程是 ( )
| A.x+y+3=0 | B.2x-y-5="0" | C.3x-y-9=0 | D.4x-3y+7=0 |
直线 被圆
被圆 截得的线段的长为( )
截得的线段的长为( )
| A.2 | B. | C. | D.1 |
若直线 经过点
经过点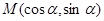 ,则 ( )
,则 ( )
A. . . | B. . . |
C. . . | D. . . |
已知圆的方程为(x-3)2+y2=9,则圆心坐标为( )
| A.(3,0) | B.(-3,0) | C.(0,3) | D.(0,-3) |
已知圆C: 和点
和点 ,P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。
,P是圆上一点,线段BP的垂直平分线交CP于M点,则M点的轨迹方程是( )。
A. . . | B. |
C. | D. |
已知集合 ,
,


 。若存在实数
。若存在实数 使得
使得 成立,称点
成立,称点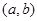 为“£”点,则“£”点在平面区域
为“£”点,则“£”点在平面区域 内的个数是
内的个数是
| A.0 | B.1 | C.2 | D.无数个 |