题目内容
与直线 和圆
和圆 都相切的半径最小的圆的方程是( )
都相切的半径最小的圆的方程是( )
A. | B. |
C. | D. |
C
解析试题分析:根据题意,圆 的圆心(-1,1)半径为
的圆心(-1,1)半径为 ,那么由于直线
,那么由于直线 和圆
和圆 相离,则可知最小的圆的圆心为(1,-1),而且半径为
相离,则可知最小的圆的圆心为(1,-1),而且半径为 ,那么可知圆的方程为
,那么可知圆的方程为 ,选C。
,选C。
考点:直线与圆
点评:主要是考查了直线与圆的位置关系的运用,属于基础题。

练习册系列答案
相关题目
若直线 与曲线
与曲线 有且只有两个公共点,则m的取值范围是( )
有且只有两个公共点,则m的取值范围是( )
A. | B. | C. | D. |
已知直线 经过点
经过点 ,当
,当 截圆
截圆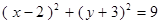 所得弦长最长时,直线
所得弦长最长时,直线 的方程为( )
的方程为( )
A. | B. |
C.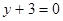 | D. |
方程x2+y2+2ax-by+c=0表示圆心为C(2,2),半径为2的圆,则a、b、c的值依次为( )
| A.2、4、4 | B.-2、4、4 | C.2、-4、4 | D.2、-4、-4 |
已知圆 在曲线
在曲线 的内部,则半径
的内部,则半径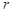 的范围是( )
的范围是( )
A.0<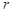 < < | B.0<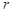 <2 <2 | C.0<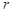 <2 <2 | D.0<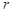 <4 <4 |
过点A(1,-1)、B(-1,1)且圆心在直线x+y-2=0上的圆的方程是( )
| A.(x-3)2+(y+1)2=4 | B.(x+3)2+(y-1)2=4 |
| C.(x-1)2+(y-1)2=4 | D.(x+1)2+(y+1)2=4 |
若直线 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )
A. | B. | C. | D. 或 或 |
直线 与圆
与圆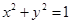 的位置关系为( )
的位置关系为( )
| A.相切 | B.相交但直线不过圆心 |
| C.直线过圆心 | D.相离 |
圆:x²+y²-4x+6y=0和圆:x²+y²-6x=0交于A,B两点,则AB的垂直平分线的方程是 ( )
| A.x+y+3=0 | B.2x-y-5="0" | C.3x-y-9=0 | D.4x-3y+7=0 |