题目内容
11.下列否定不正确的是( )| A. | “?x∈R,x2>0”的否定是“?x0∈R,x02≤0” | |
| B. | “?x0∈R,x02<0”的否定是“?x∈R,x2<0” | |
| C. | “?θ0∈R,sinθ0+cosθ0<1”的否定是“?θ∈R,sinθ+cosθ≥1” | |
| D. | “?θ∈R,sinθ≤1”的否定是?θ0∈R,sinθ0>1 |
分析 根据全称命题和特称命题否定的方法,写出各个命题的否定,可得结论.
解答 解:“?x∈R,x2>0”的否定是“?x0∈R,x02≤0”,故A正确;
“?x0∈R,x02<0”的否定是“?x∈R,x2≥0”,故B错误;
“?θ0∈R,sinθ0+cosθ0<1”的否定是“?θ∈R,sinθ+cosθ≥1”,故C正确;
“?θ∈R,sinθ≤1”的否定是?θ0∈R,sinθ0>1,故D正确;
故选:B
点评 本题以命题的真假判断与应用为载体,考查了全称命题,特称命题的否定,难度中档.

练习册系列答案
相关题目
1.设f(x)是定义在R上的偶函数,对x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=($\frac{1}{2}$)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是( )
| A. | (2,3) | B. | $(\root{3}{3},2)$ | C. | $(\root{3}{4},2)$ | D. | $(\root{3}{2},3)$ |
2.函数f(x)=xlnx的单调递减区间为( )
| A. | $(0,\frac{1}{e})$ | B. | $(-∞,\frac{1}{e})$ | C. | (-∞,-e) | D. | $(\frac{1}{e},+∞)$ |
19.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,满足|$\overrightarrow{b}$|=4|$\overrightarrow{a}$|,且$\overrightarrow{a}$⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
3.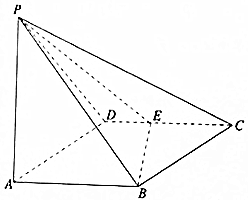 如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角B-PE-D的余弦值.
 如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.
如图所示,四棱锥P-ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2.(Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求二面角B-PE-D的余弦值.
8.已知直线l经过点(0,-2),其倾斜角的大小是60°,则直线l与两坐标轴围成三角形的面积S等于( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\frac{{3\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |