题目内容
(本小题满分14分)
如图,四棱锥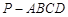 的底面
的底面 为菱形,
为菱形,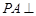 平面
平面 ,
,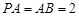 , E、F分别为
, E、F分别为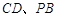 的中点,
的中点,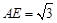 .
.

(Ⅰ)求证:平面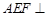 平面
平面 .
.
(Ⅱ)求平面 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
如图,四棱锥
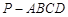 的底面
的底面 为菱形,
为菱形,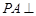 平面
平面 ,
,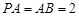 , E、F分别为
, E、F分别为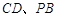 的中点,
的中点,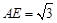 .
.
(Ⅰ)求证:平面
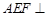 平面
平面 .
.(Ⅱ)求平面
 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.(Ⅰ)先证得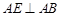 .
.
再证得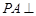
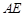 .由
.由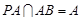 ,证出
,证出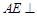 平面
平面 ,所以,平面
,所以,平面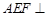 平面
平面 .
.
(Ⅱ)平面 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为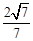 .
.
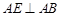 .
. 再证得
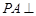
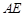 .由
.由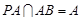 ,证出
,证出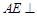 平面
平面 ,所以,平面
,所以,平面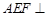 平面
平面 .
. (Ⅱ)平面
 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为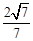 .
. 试题分析:(Ⅰ)∵四边形
 是菱形,
是菱形,∴
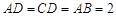 .
.在
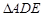 中,
中,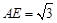 ,
,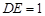 ,
,∴
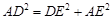 .
.∴
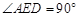 ,即
,即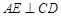 .
.又
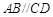 , ∴
, ∴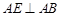 .…………………2分
.…………………2分∵
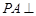 平面
平面 ,
,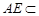 平面
平面 ,
,∴
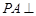
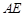 .又∵
.又∵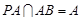 ,
,∴
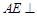 平面
平面 ,………………………………………4分
,………………………………………4分又∵
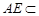 平面
平面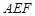 ,
,平面
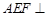 平面
平面 . ………………………………6分
. ………………………………6分(Ⅱ)解法一:由(1)知
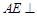 平面
平面 ,而
,而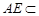 平面
平面 ,
,∴平面
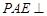 平面
平面 ………………………7分
………………………7分∵
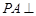 平面
平面 ,∴
,∴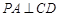 .
.由(Ⅰ)知
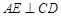 ,又
,又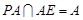
∴
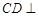 平面
平面 ,又
,又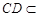 平面
平面 ,
,∴平面
 平面
平面 .…………………………9分
.…………………………9分∴平面
 是平面
是平面 与平面
与平面 的公垂面.
的公垂面.所以,
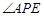 就是平面
就是平面 与平面
与平面 所成的锐二面角的平面角.……10分
所成的锐二面角的平面角.……10分在
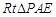 中,
中,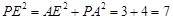 ,即
,即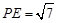 .……………11分
.……………11分又
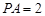 ,
,∴
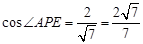 .
.所以,平面
 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为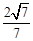 .…………14分
.…………14分
理(Ⅱ)解法二:以
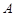 为原点,
为原点,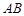 、
、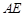 分别为
分别为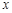 轴、
轴、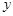 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系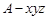 ,如图所示.因为
,如图所示.因为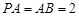 ,
,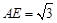 ,所以,
,所以,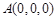 、
、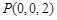 、
、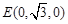 、
、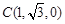 ,…………7分
,…………7分则
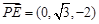 ,
,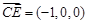 ,
,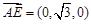 .………8分
.………8分由(Ⅰ)知
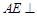 平面
平面 ,
,故平面
 的一个法向量为
的一个法向量为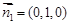 .……………………9分
.……………………9分设平面
 的一个法向量为
的一个法向量为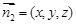 ,
,则
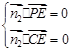 ,即
,即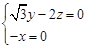 ,令
,令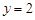 ,
,则
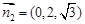 . …………………11分
. …………………11分∴
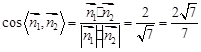 .
.所以,平面
 与平面
与平面 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为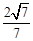 .……14分
.……14分点评:典型题,立体几何题,是高考必考内容,往往涉及垂直关系、平行关系、角、距离、体积的计算。在计算问题中,有“几何法”和“向量法”。利用几何法,要遵循“一作、二证、三计算”的步骤,本题解法较多二应用向量则简化了证明过程。

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
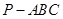 中,
中, 面
面 ,
, 是直角三角形,
是直角三角形, ,
, ,
, ,点
,点 分别为
分别为 的中点。
的中点。
 ;
; 与平面
与平面 所成的角的大小;
所成的角的大小; 的正切值。
的正切值。 、
、 ,能判定
,能判定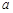

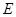 是
是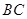 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持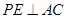 .则动点
.则动点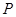 的轨迹与△
的轨迹与△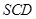 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )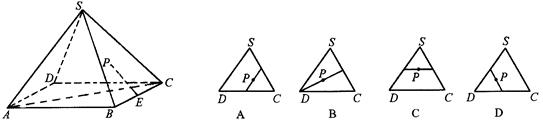
 中,E,F满足
中,E,F满足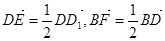 .
.
 ;
; ;
; 与矩形
与矩形 所在的平面互相垂直,将
所在的平面互相垂直,将 沿
沿 翻折,翻折后的点E恰与BC上的点P重合.设
翻折,翻折后的点E恰与BC上的点P重合.设 ,
, ,
, ,则当
,则当 __时,
__时, 有最小值.
有最小值.




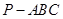 中,
中,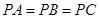 ,
,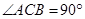 ,
,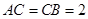 .
. 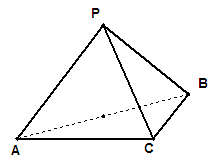
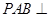 平面
平面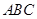 ;
;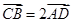 ,且异面直线
,且异面直线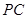 与
与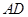 的夹角为
的夹角为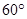 时,求二面角
时,求二面角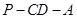 的余弦值.
的余弦值. 中,底面
中,底面 是正方形,侧面
是正方形,侧面 是正三角形,且平面
是正三角形,且平面
 ⊥平面
⊥平面 与底面
与底面 ,求点
,求点 到平面
到平面 的距离.
的距离.