题目内容
20．在平面直角坐标系中，若不等式组$\left\{\begin{array}{l}x+2y≥2\\ 1≤x≤2\\ ax-y+1≥0\end{array}\right.$（a为常数）表示的区域面积等于1，则a的值为（ ）| A． | $-\frac{1}{6}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{2}$ | D． | 1 |
分析 本题主要考查线性规划的基本知识，先画出约束条件$\left\{\begin{array}{l}x+2y≥2\\ 1≤x≤2\\ ax-y+1≥0\end{array}\right.$的可行域，根据已知条件中，表示的平面区域的面积等于2，构造关于a的方程，解方程即可得到答案．
解答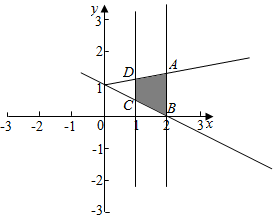 
解：不等式组$\left\{\begin{array}{l}x+2y≥2\\ 1≤x≤2\\ ax-y+1≥0\end{array}\right.$所围成的区域如图ABCD所示，
∵其面积为1，A（2，2a+1），B（2，0），C（1，$\frac{1}{2}$），D（1，a+1）
∴SABCD=$\frac{2a+1+a+\frac{1}{2}}{2}×1$=1，
解得a=$\frac{1}{6}$．
故选：B．
点评 平面区域的面积问题是线性规划问题中一类重要题型，在解题时，关键是正确地画出平面区域，然后结合有关面积公式求解．
练习册系列答案
相关题目
10．已知集合A={x|x2-x-6＞0}，集合$B=\{y\left|{y=\sqrt{{x^2}+2x+10}}\right.\}$，全集U=R，则（∁UB）∩A为（ ）
| A． | （-∞，-2） | B． | （2，3） | C． | （3，+∞） | D． | （1，+∞） |
8．设m＞0，双曲线M：$\frac{{x}^{2}}{m}$-y2=1与圆N：x2+（y-m）2=1相切，A（-$\sqrt{m+1}$，0），B（$\sqrt{m+1}$，0），若圆N上存在一点P满足|PA|-|PB|=2$\sqrt{m}$．则点P到x轴的距离为（ ）
| A． | m3 | B． | m2 | C． | m | D． | $\frac{m}{1+m}$ |
5．已知曲线y=x-1与直线x=1，x=3，x轴围成的封闭区域为A，直线x=1，x=3，y=0，y=1围成的封闭区域为B，在区域B内任取一点P，该点P落在区域A的概率为$\frac{ln3}{2}$．
12．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1，的离心率e=2，若过双曲线右焦点且与渐近线平行的直线与圆x2+y2+4x=8相切，则双曲线的方程为（ ）
| A． | x2-$\frac{{y}^{2}}{3}$=1 | B． | $\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{6}$=1 | C． | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{9}$=1 | D． | $\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{12}$=1 |