题目内容
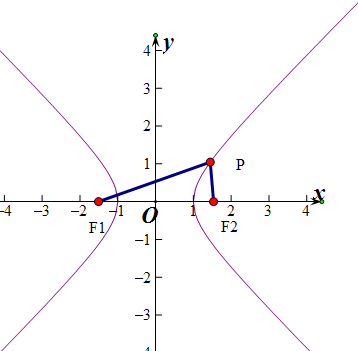
设F1,F2为双曲线x2-y2=1的左右焦点,P是双曲线上在x轴上方的点,∠F1PF2为直角,则sinPF1F2的所有可能取值之和为 .
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由|PF1|-|PF2|=2,|PF1|2+|PF2|2=8,求出:|PF1|=
+1,|PF2|=
-1,利用直角三角形即可得出sin∠PF1F2=
=
,
再利用对称性得出 另一个值
.
| 3 |
| 3 |
| ||
2
|
| ||||
| 4 |
再利用对称性得出 另一个值
| ||||
| 4 |
解答:
解:∵F1,F2为双曲线x2-y2=1的左右焦点,P是双曲线上在x轴上方的点,∠F1PF2为直角
∴|F1F2|=2
,
|PF1|-|PF2|=2,
|PF1|2+|PF2|2=8,
联合方程求解得:|PF1|=
+1,|PF2|=
-1,
∴sin∠PF1F2=
=
,
cos∠PF1F2=
=
,
根据对称性可知:当P点在坐支上时,此时的sinPF1F2=
故
+
=
,
故答案为:
.
∴|F1F2|=2
| 2 |
|PF1|-|PF2|=2,
|PF1|2+|PF2|2=8,
联合方程求解得:|PF1|=
| 3 |
| 3 |
∴sin∠PF1F2=
| ||
2
|
| ||||
| 4 |
cos∠PF1F2=
| ||
2
|
| ||||
| 4 |
根据对称性可知:当P点在坐支上时,此时的sinPF1F2=
| ||||
| 4 |

故
| ||||
| 4 |
| ||||
| 4 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题考查了双曲线的定义,焦点三角形的性质,勾股定理,双曲线的对称性,综合求解问题,属于中档题.

练习册系列答案
相关题目
一个三角形用斜二测画法所作的直观图是一个边长为1正三角形,则原三角形的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
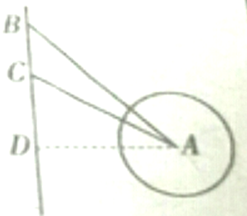 某学校组织同学们参加红色七日游--还上夏令营活动,如图,海中小岛A周围20海里内有暗礁,夏令营的船只正向南航行,在B处测得小岛A在船的南偏东30°;航行30海里后,在C处测得小岛A在船的南偏东60°,如果此船不改变航向,继续向南航行,有无触礁危险?
某学校组织同学们参加红色七日游--还上夏令营活动,如图,海中小岛A周围20海里内有暗礁,夏令营的船只正向南航行,在B处测得小岛A在船的南偏东30°;航行30海里后,在C处测得小岛A在船的南偏东60°,如果此船不改变航向,继续向南航行,有无触礁危险?