题目内容
3.正方体ABCD-A1B1C1D1中,E为AC的中点.证明:(1)BD1⊥AC;(2)BD1⊥EB1.分析 (1)以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系Dxyz,可求$\overrightarrow{B{D}_{1}}$=(-1,-1,1),$\overrightarrow{AC}$=(-1,1,0),由$\overrightarrow{B{D}_{1}}•\overrightarrow{AC}$=0,即可证明BD1⊥AC.
(2)由(1)可求$\overrightarrow{B{D}_{1}}$=(-1,-1,1),$\overrightarrow{E{B}_{1}}$=($\frac{1}{2}$,$\frac{1}{2}$,1),由$\overrightarrow{B{D}_{1}}$•$\overrightarrow{E{B}_{1}}$=0,即可证明BD1⊥EB1.
解答 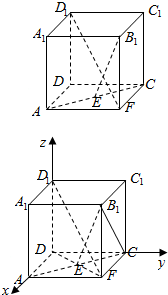 证明:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系Dxyz,
证明:以D为原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系Dxyz,
设正方体的棱长为1,则B(1,1,0),D1(0,0,1),A(1,0,0),C(0,1,0),E($\frac{1}{2}$,$\frac{1}{2}$,0),B1(1,1,1),
(1)$\overrightarrow{B{D}_{1}}$=(-1,-1,1),$\overrightarrow{AC}$=(-1,1,0),
∴$\overrightarrow{B{D}_{1}}•\overrightarrow{AC}$=(-1)×(-1)+(-1)×1+1×0=0,
∴$\overrightarrow{B{D}_{1}}$⊥$\overrightarrow{AC}$
∴BD1⊥AC.
(2)$\overrightarrow{B{D}_{1}}$=(-1,-1,1),$\overrightarrow{E{B}_{1}}$=($\frac{1}{2}$,$\frac{1}{2}$,1),
∴$\overrightarrow{B{D}_{1}}$•$\overrightarrow{E{B}_{1}}$=(-1)×$\frac{1}{2}$+(-1)×$\frac{1}{2}$+1×1=0,
∴$\overrightarrow{B{D}_{1}}$⊥$\overrightarrow{E{B}_{1}}$,
∴BD1⊥EB1.
点评 本题主要考查了直线与平面垂直的性质,考查了空间想象能力和推理论证能力,建立空间直角坐标系,用向量求解是解题的关键,属于中档题.

| A. | -10 | B. | 10 | C. | -10$\sqrt{3}$ | D. | 10$\sqrt{3}$ |
| A. | -16 | B. | 16 | C. | 8 | D. | -8 |
| A. | (-∞,1] | B. | (0,1] | C. | [1,+∞) | D. | [0,1] |
| A. | 既不充分也不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 充分不必要条件 |

| A. | 8πcm2 | B. | 7πcm2 | C. | 6πcm2 | D. | 5πcm2 |