题目内容
20.已知数列{an}各项均为正,若a1=1,且lgan+1+lgan=lg(an-an+1)(n∈N*).(1)求数列{an}的通项公式;
(2)设数列{$\frac{{a}_{n}}{n+1}$}的前n项和Sn,求Sn的取值范围.
分析 (1)由对数运算法则得到an+1an=an-an+1,从而$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=1,$\frac{1}{{a}_{1}}=1$,由此能求出数列{an}的通项公式.
(2)由$\frac{{a}_{n}}{n+1}$=$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$,利用裂项求和法求出数列{$\frac{{a}_{n}}{n+1}$}的前n项和,由此能求出Sn的取值范围.
解答 解:(1)∵数列{an}各项均为正,a1=1,且lgan+1+lgan=lg(an-an+1)(n∈N*),
∴an+1an=an-an+1,∴$\frac{1}{{a}_{n+1}}-\frac{1}{{a}_{n}}$=1,$\frac{1}{{a}_{1}}=1$,
∴{$\frac{1}{{a}_{n}}$}是以1为首项,公差为1的等差数列,
∴$\frac{1}{{a}_{n}}$=1+(n-1)•1=n,
∴数列{an}的通项公式${a}_{n}=\frac{1}{n}$.
(2)∵$\frac{{a}_{n}}{n+1}$=$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$,
∴数列{$\frac{{a}_{n}}{n+1}$}的前n项和:
Sn=1-$\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{n}-\frac{1}{n+1}$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$.
n=1时,(Sn)min=1-$\frac{1}{1+1}$=$\frac{1}{2}$,Sn=1-$\frac{1}{n+1}$<1,
∴Sn的取值范围是[$\frac{1}{2},1$).
点评 本题考查数列的通项公式的求法,考查数列的前n项和的取值范围的求法,是中档题,解题时要认真审题,注意等差数列的性质、对数运算法则、裂项求和法的合理运用.

| A. | x0<-1或x0>1 | B. | -log23<x0<1 | C. | x0<-1 | D. | x0<-log23或x0>1 |
| A. | 充分不必要 | B. | 必要不充分 | C. | 充要 | D. | 都不是 |
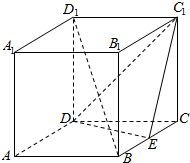 如图,在正方体ABCD-A1B1C1D1中,E是棱BC的中点.
如图,在正方体ABCD-A1B1C1D1中,E是棱BC的中点.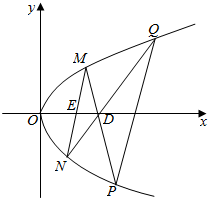 如图,在平面直角坐标系中,已知抛物线C:y2=2px(p>0).设点D(n,0),E(m,0).M为抛物线C上的动点(异于顶点),连接ME并延长交抛物线C于点N,连接MD、ND并延长交抛物线C于点P、Q,连接PQ.设直线MN、PQ的斜率存在且分别为k1,k2.
如图,在平面直角坐标系中,已知抛物线C:y2=2px(p>0).设点D(n,0),E(m,0).M为抛物线C上的动点(异于顶点),连接ME并延长交抛物线C于点N,连接MD、ND并延长交抛物线C于点P、Q,连接PQ.设直线MN、PQ的斜率存在且分别为k1,k2.