题目内容
已知向量
=（1，1），
=（0，-2），在下列条件下分别求k的值；
（1）
+
与k
-
平行；
（2）
+
与k
-
夹角为120°．
| a |
| b |
（1）
| a |
| b |
| a |
| b |
（2）
| a |
| b |
| a |
| b |
考点：平面向量数量积的运算,平行向量与共线向量
专题：平面向量及应用
分析：利用坐标表示两问的向量坐标，然后利用向量平行以及数量积公式解答．
解答：
解：（1）由已知
+
=（1，-1），k
-
=（k，k+2），又
+
与k
-
平行，所以-k=k+2，解得k=-1；
（2）
+
与k
-
夹角为120°，所以（
+
）•（k
-
）=|
+
||
-
|cos120°，
即-2=-
×
×
，解得k=-1±
．
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
（2）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
即-2=-
| 2 |
| k2+(k+2)2 |
| 1 |
| 2 |
| 3 |
点评：本题考查了向量的坐标运算以及向量平行的坐标关系、数量积公式的运用；属于基础题．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
与y轴相切并和圆x2+y2-10x=0外切的动圆圆心的轨迹是 （ ）
| A、圆 | B、抛物线 |
| C、双曲线 | D、抛物线和一条射线 |
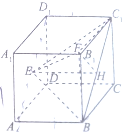已知正方体ABCD-A1B1C1D1棱长为1，E、F、H分别为面A1ADD1、面DCC1D1与面BCC1B1的中心．