题目内容
7.已知函数f(x)=lnx-a(x-1),g(x)=ex(1)求当a=1时,函数f(x)的单调区间;
(2)过原点分别作曲线y=f(x)与y=g(x)的切线l1、l2,已知两切线的斜率互为倒数,证明:a=0或$\frac{e-1}{e}$<a<$\frac{{e}^{2}-1}{e}$.
分析 (1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)设出切线方程以及切点坐标,根据函数的单调性证明即可.
解答 解:(1)当a=1时,${f^/}(x)=\frac{1}{x}-1=\frac{1-x}{x}(x>0)$.
当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0,
所以,函数f(x)的单调递增区间是(0,1),单调递减区间是(1,+∞).…(5分)
(2)解法1 设切线l2的方程为y=k2x,切点为(x2,y2),
则${y_2}={e^{x_2}}$,${k_2}={g^/}({x_2})$=${e^{x_2}}=\frac{y_2}{x_2}$,所以x2=1,y2=e,于是${k_2}={e^{x_2}}=e$,
由题意知,切线l1的斜率为${k_1}=\frac{1}{k_2}=\frac{1}{e}$,l1的方程为$y={k_1}x=\frac{1}{e}x$.
设l1与曲线y=f(x)的切点为(x1,y1),
则${k_1}={f^/}({x_1})=\frac{1}{x_1}-a=\frac{1}{e}=\frac{y_1}{x_1}$,所以${y_1}=\frac{x_1}{e}=1$-ax1,$a=\frac{1}{x_1}-\frac{1}{e}$.
又因为y1=lnx1-a(x1-1),消去y1和a后,整理得$ln{x_1}-1+\frac{1}{x_1}-\frac{1}{e}=0$.
令$m(x)=lnx-1+\frac{1}{x}-\frac{1}{e}$,则${m^/}(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$,
m(x)在(0,1)上单调递减,在(1,+∞)上单调递增.
若x1∈(0,1),因为$m(\frac{1}{e})=-2+e-\frac{1}{e>0\;}\;,\;m(1)=-\frac{1}{e}<0$,
所以${x_1}∈(\frac{1}{e}\;,\;1)$,而$a=\frac{1}{x_1}-\frac{1}{e}$在${x_1}∈(\frac{1}{e}\;,\;1)$上单调递减,所以$\frac{e-1}{e}<a<\frac{{{e^2}-1}}{e}$.
若x1∈(1,+∞),因为m(x)在(1,+∞)上单调递增,且m(e)=0,
所以x1=e,所以$a=\frac{1}{x_1}-\frac{1}{e}$=0.
综上可知:a=0或$\frac{e-1}{e}<a<\frac{{{e^2}-1}}{e}$.…(12分)
解法2 设切线l2的方程为y=k2x,切点为(x2,y2),
则${y_2}={e^{x_2}}$,${k_2}={g^/}({x_2})$=${e^{x_2}}=\frac{y_2}{x_2}$,
所以x2=1,y2=e,于是${k_2}={e^{x_2}}=e$,
由题意知,切线l1的斜率为${k_1}=\frac{1}{k_2}=\frac{1}{e}$,l1的方程为$y={k_1}x=\frac{1}{e}x$.
设l1与曲线y=f(x)的切点为(x1,y1),
则${k_1}={f^/}({x_1})=\frac{1}{x_1}-a=\frac{1}{e}=\frac{y_1}{x_1}$,所以$a=\frac{1}{x_1}-\frac{1}{e}$.
又因为y1=lnx1-a(x1-1),所以$\frac{1}{x_1}-a=\frac{{ln{x_1}-a({x_1}-1)}}{x_1}$,
所以$ln{x_1}=1-a\;,\;{x_1}={e^{1-a}}$,消去x1得ea-ae-1=0.
令p(a)=ea-ae-1,则p′(a)=ea-e,
p(a)在(-∞,1)上递减,在(1,+∞)上递增.
当a∈(-∞,1)时,因为p(0)=0,所以a=0.
当a∈(1,+∞)时,因为p(1)=-1<0,
p(2)=e2-2e-1>0,所以1<a<2,
而$\frac{e-1}{e}<1$,$\frac{{{e^2}-1}}{e}>2$,所以$\frac{e-1}{e}<a<$$\frac{{{e^2}-1}}{e}$,
综上可知:a=0或$\frac{e-1}{e}<a<\frac{{{e^2}-1}}{e}$.…(12分)
点评 本题考查了函数的单调性问题,考查导数的应用以及切线的切线方程问题,考查转化思想,是一道综合题.

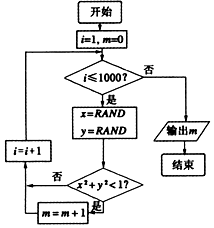 我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为781,则由此可估计π的近似值为( )
我们可以用随机模拟的方法估计π的值,如图程序框图表示其基本步骤(函数RAND是产生随机数的函数,它能随机产生(0,1)内的任何一个实数).若输出的结果为781,则由此可估计π的近似值为( )| A. | 3.119 | B. | 3.124 | C. | 3.132 | D. | 3.151 |
| A. | -1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
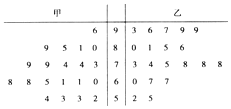 某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.
某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人,陈老师采用A、B两种不同的数学方式分别在甲、乙两个班级进行教改实验,为了解教学效果,期末考试后,陈老师利用随机抽样的方法分别从两个班级中各随机抽取20名学生,并对他们的成绩进行统计,作出茎叶图如图,记成绩不低于90分者为“成绩优秀”.(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个均“成绩优秀”的概率;
(2)由以上统计数据填写下面列联表,并判断是否有90%的把握认为“成绩优秀”与教学方式有关.
| 甲班(A方式) | 乙班(B方式) | 总 计 | |
| 成绩优秀 | 1 | 5 | 6 |
| 成绩不优秀 | 19 | 15 | 34 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
| x | 0 | 1 | m | 3 |
| y | 1 | 3 | 5 | n |
| A. | $(\frac{1}{2},1]$ | B. | $(0,\frac{2}{3})$ | C. | $(\frac{2}{3},1]$ | D. | $(\frac{1}{2},\frac{2}{3})$ |
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{4}$ | D. | $\frac{3}{4}$ |
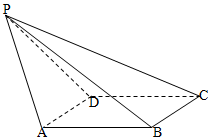 如图,已知四边形ABCD为菱形,平面ABCD外一点P,PB⊥AD,△PAD为边长等于2的正三角形,且PB在平面ABCD的射影长等于$\frac{3}{2}\sqrt{3}$.
如图,已知四边形ABCD为菱形,平面ABCD外一点P,PB⊥AD,△PAD为边长等于2的正三角形,且PB在平面ABCD的射影长等于$\frac{3}{2}\sqrt{3}$.