我们可以用随机模拟的方法估计π的值.如图程序框图表示其基本步骤(函数RAND是产生随机数的函数.它能随机产生．若输出的结果为781.则由此可估计π的近似值为( )A．3.119B．3.124C．3.132D．3.151 题目和参考答案——青夏教育精英家教网—

题目内容

17．

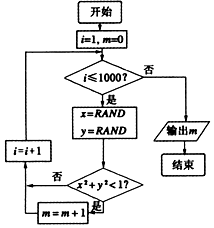我们可以用随机模拟的方法估计π的值，如图程序框图表示其基本步骤（函数RAND是产生随机数的函数，它能随机产生（0，1）内的任何一个实数）．若输出的结果为781，则由此可估计π的近似值为（　　）

A．

3.119

B．

3.124

C．

3.132

D．

3.151

分析我们可分析出程序的功能是利用随机模拟实验的方法求任取（0，1）上的x，y，z，求x²+y²＜1的概率，计算x²+y²+＜1发生的概率，代入几何概型公式，即可得到答案．

解答解：x²+y²＜1发生的概率为$π•{1}^{2}•\frac{1}{4}$=$\frac{π}{4}$，当输出结果为781时，i=1001，m=781，x²+y²＜1发生的概率为P=$\frac{781}{1000}$，∴$\frac{781}{1000}$=$\frac{π}{4}$，即π=3.124，
故选B．

点评本题考查了程序框图的应用问题和随机模拟法求圆周率的问题，也考查了几何概率的应用问题，是综合题．

练习册系列答案

相关题目

17．执行如图程序框图，则输出的S值为（　　）

8．已知定义在R上的函数f（x）=Acos（ωx+φ）（A＞0，ω＞0，|φ|≤$\frac{π}{2}$），满足：最大值为2，其图象相邻两个最低点之间距离为π，且函数f（x）的图象关于点（$\frac{π}{12}$，0）对称．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若向量$\overrightarrow{a}$=（f（x-$\frac{π}{6}$），1），$\overrightarrow{b}$=（$\frac{1}{2}$，-2cosx），$x∈[-\frac{3π}{4}，\frac{π}{2}]$，设函数$g（x）=\overrightarrow a•\overrightarrow b+\frac{1}{2}$，求函数g（x）的值域．

5．已知函数f（x）=|x+1|
（1）解不等式f（x）＞4-|x-1|；
（2）已知a+b=1（a＞0，b＞0），若|x-m|-f（x）≤$\frac{4}{a}$+$\frac{1}{b}$（m＞0）对任意的x∈R恒成立，求实数m的取值．

12．已知$\overrightarrow{a}$，$\overrightarrow{b}$是不共线的两个向量，且$\overrightarrow{a}$$•\overrightarrow{b}$＞0，|$\overrightarrow{b}$|≥4，若对任意m，n∈R，|$\overrightarrow{a}$+m$\overrightarrow{b}$|的最小值是1，|$\overrightarrow{b}$+n$\overrightarrow{a}$|的最小值是2，则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影的最小值是$\sqrt{3}$．

2．如图是一个算法的流程图，若输入的x的值为1，则输出的S的值为100

9．以下是某地搜集到的新房屋的销售价格y与房屋的面积x的数据：

房屋面积（m²）	115	110	80	135	105
销售价格（万元）	24.8	21.6	18.4	29.2	22

数据对应的散点图如图所示；
（1）求线性回归方程．（参考公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$）
（参考数据 $\overline{x}$=$\frac{1}{5}$$\sum_{i=1}^{5}$x_i=109，$\sum_{i=1}^{5}$（x_i-$\overline{x}$）²=1570，$\sum_{i=1}^{5}$（x_i-$\overline{x}$）（y_i-$\overline{y}$）=311.2）
（2）据（1）的结果估计当房屋面积为150m²时的销售价格．

6．已知四面体ABCD的六条棱中，AC=BD=4，其余的四条棱的长都是3，则此四面体的外接球的表面积为（　　）

7．已知函数f（x）=lnx-a（x-1），g（x）=e^x
（1）求当a=1时，函数f（x）的单调区间；
（2）过原点分别作曲线y=f（x）与y=g（x）的切线l₁、l₂，已知两切线的斜率互为倒数，证明：a=0或$\frac{e-1}{e}$＜a＜$\frac{{e}^{2}-1}{e}$．

试题分类