题目内容
12.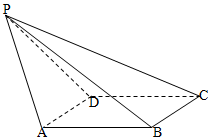 如图,已知四边形ABCD为菱形,平面ABCD外一点P,PB⊥AD,△PAD为边长等于2的正三角形,且PB在平面ABCD的射影长等于$\frac{3}{2}\sqrt{3}$.
如图,已知四边形ABCD为菱形,平面ABCD外一点P,PB⊥AD,△PAD为边长等于2的正三角形,且PB在平面ABCD的射影长等于$\frac{3}{2}\sqrt{3}$.(I)求点P到平面ABCD的距离;
(II)求PC与平面ABCD所成角的正切值.
分析 (Ⅰ)设P在平面ABCD的射影为E,连BE交AD于O点,推导出△ABD为正三角形.由此能求出点P到平面ABCD的距离.
(Ⅱ)在直角△EBC中,求出CE,由此能求出PC与平面ABCD所成的角θ的正切值.
解答 解:(Ⅰ)设P在平面ABCD的射影为E,连BE交AD于O点,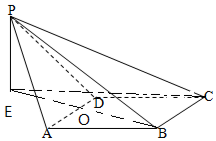
由题意知EB⊥AD,
∴PO⊥AD,OE⊥AD,∴O为AD的中点,
∴△ABD为正三角形.
∴OE=$\frac{3}{2}\sqrt{3}-\sqrt{3}=\frac{{\sqrt{3}}}{2}$.PE=$\sqrt{3}$,
∴$cos∠POE=\frac{OE}{PE}=\frac{1}{2}$,∴∠POE=60°,
∴点P到平面ABCD的距离$d=PE=PO×sin{60°}=\sqrt{3}×\frac{{\sqrt{3}}}{2}=\frac{3}{2}$.
(Ⅱ)在直角△EBC中,
$EC=\sqrt{E{B^2}+B{C^2}}=\sqrt{{{(\frac{{3\sqrt{3}}}{2})}^2}+{2^2}}=\frac{{\sqrt{43}}}{2}$
∴PC与平面ABCD所成的角θ的正切值为:
$tanθ=\frac{PE}{EC}=\frac{{3\sqrt{43}}}{43}$.
点评 本题考查点到平面的距离、线面角的正切值的求法,考查空间中线线、线面、面面的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力、数据处理能力,考查函数与方程思想、化归与转化思想、数形结合,考查创新意识、应用意识,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设a=${∫}_{0}^{π}$(sinx+cosx)dx,且二项式(a$\sqrt{x}$-$\frac{1}{\sqrt{x}}$)n的所有二项式系数之和为64,则其展开式中含x2项的系数是( )
| A. | -192 | B. | 192 | C. | -6 | D. | 6 |
20.若$α,β∈({-\frac{π}{2},\frac{π}{2}})$,且tanα,tanβ是方程${x^2}+4\sqrt{3}x+5=0$的两个根,则α+β等于( )
| A. | $\frac{π}{3}$或$\frac{4π}{3}$ | B. | $\frac{π}{3}$或$-\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $-\frac{2π}{3}$ |

