题目内容
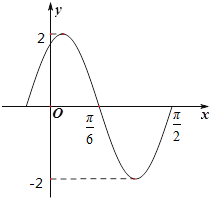
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象如图，求f（
）的值．
| π |
| 4 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式
专题：三角函数的图像与性质
分析：由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，可得f（x）的解析式，从而求得f（
）的值．
| π |
| 4 |
解答：
解；由函数的图象可得A=2，
=
=
-
=
，∴ω=3．
再根据五点法作图可得3×
+φ=π，求得φ=
，∴f（x）=2sin（3x+
）=2cos3x，
∴f（
）=2cos
=-2cos
=-
．
| T |
| 2 |
| π |
| ω |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
再根据五点法作图可得3×
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
∴f（
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| 2 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，属于基础题．
练习册系列答案
相关题目
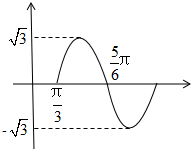已知函数y=Asin（ωx+φ）（A＞0，ω＞0），一个周期内的函数图象，如图所示，求：
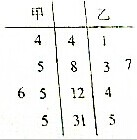根据空气质量指数API（整数）的不同，可将空气质量分级如下表：