题目内容
设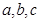 都是正实数,且
都是正实数,且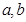 满足
满足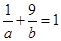 ,则使
,则使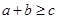 恒成立的
恒成立的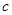 的范围是( )
的范围是( )
| A.(0,8] | B.(0,10] | C.(0,12] | D.(0,16] |
D.
解析试题分析:由已知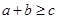 恒成立,
恒成立,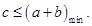 由已知及均值不等式可得
由已知及均值不等式可得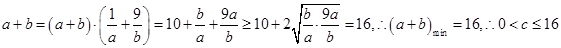 ,故选D.
,故选D.
考点:1.均值不等式;2.恒成立问题中的参数取值范围问题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设a,b是两个实数,且a≠b,① ②
② ,③
,③ 。上述三个式子恒成立的有( )
。上述三个式子恒成立的有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
若正实数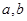 满足
满足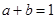 ,则
,则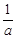 +
+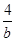 的最小值是( )
的最小值是( )
| A.4 | B.6 | C.8 | D.9 |
若 且
且 ,使不等式
,使不等式 ≥
≥ 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. ≤ ≤ | B. ≤ ≤ | C. ≥ ≥ | D. ≥ ≥ |
函数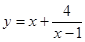
 的最小值是( )
的最小值是( )
| A.3 | B.4 | C.5 | D.6 |
设 是正实数,以下不等式
是正实数,以下不等式
① 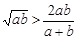 ,②
,② 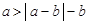 ,③
,③  ,④
,④  恒成立的序号为( )
恒成立的序号为( )
| A.①、③ | B.①、④ | C.②、③ | D.②、④ |
若 ,且
,且 ,则下列不等式中,恒成立的是( )
,则下列不等式中,恒成立的是( )
A. | B. | C. | D. |
若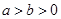 ,则代数式
,则代数式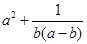 的最小值为( )
的最小值为( )
| A.2 | B.3 | C.4 | D.5 |
已知f(x)=log2(x-2),若实数m,n满足f(m)+f(2n)=3,则m+n的最小值为( )
| A.5 | B.7 | C.8 | D.9 |