题目内容
若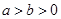 ,则代数式
,则代数式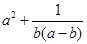 的最小值为( )
的最小值为( )
| A.2 | B.3 | C.4 | D.5 |
C
解析试题分析:

当且仅当 即
即 时等号成立
时等号成立
考点:均值不等式求最值
点评:本题主要应用不等式 求解最值,题目中两次用到了不等式性质,只有两等号同时成立时才能取得最值
求解最值,题目中两次用到了不等式性质,只有两等号同时成立时才能取得最值

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
设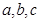 都是正实数,且
都是正实数,且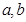 满足
满足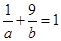 ,则使
,则使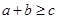 恒成立的
恒成立的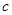 的范围是( )
的范围是( )
| A.(0,8] | B.(0,10] | C.(0,12] | D.(0,16] |
已知点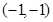 在直线
在直线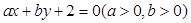 上,则
上,则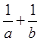 的最小值为( )
的最小值为( )
| A.1 | B.2 | C.3 | D.4 |
已知正实数 ( )
( )
| A.6 | B.8 | C.9 | D.16 |
若 ,且
,且 .则
.则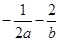 的最大值是( )
的最大值是( )
A.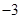 | B. | C.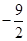 | D. |
设 ,则
,则 三数中( )
三数中( )
| A.至少有一个不大于2 | B.都小于2 |
| C.至少有一个不小于2 | D.都大于2 |
已知 ,函数
,函数 的最小值是 ( )
的最小值是 ( )
| A.5 | B.4 | C.8 | D.6 |
若 ,则函数
,则函数 的最小值为( )
的最小值为( )
A. | B. | C. | D.非上述情况 |
函数 在区间
在区间 上的最小值是( )
上的最小值是( )
A. | B. | C. | D. |