题目内容
已知定义域为R的函数 满足:
满足: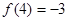 ,且对任意
,且对任意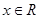 总有
总有 <3,则不等式
<3,则不等式 的解集为( )
的解集为( )
A.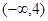 | B. | C. | D. |
D
解析试题分析:设F(x)=f(x)-(3x-15)=f(x)-3x+15,则F′(x)=f′(x)-3,由对任意x∈R总有f′(x)<3,知F′(x)=f′(x)-3<0,所以F(x)=f(x)-3x+15在R上是减函数,由此能够求出结果.解:设F(x)=f(x)-(3x-15)=f(x)-3x+15,则F′(x)=f′(x)-3,∵对任意x∈R总有f′(x)<3,∴F′(x)=f′(x)-3<0,∴F(x)=f(x)-3x+15在R上是减函数,∵f(4)=-3,∴F(4)=f(4)-3×4+15=0,∵f(x)<3x-15,∴F(x)=f(x)-3x+15<0,∴x>4.故选D.
考点:导数的运用
点评:本题考查利用导数研究函数的单调性的应用,是中档题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
已知实数a,b满足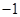 ≤a≤1,
≤a≤1,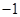 ≤b≤1,则函数
≤b≤1,则函数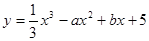 有极值的概率为( )
有极值的概率为( )
A. | B. | C.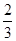 | D.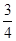 |
函数 的的单调递增区间是 ( )
的的单调递增区间是 ( )
A.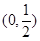 | B.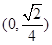 | C.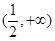 | D. 和 和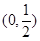 |
对于R上可导的任意函数f(x),且 若满足(x-1)
若满足(x-1) >0,则必有( )
>0,则必有( )
| A.f(0)+f(2)<2f(1) | B.f(0)+f(2)³2f(1) |
| C.f(0)+f(2)>2f(1) | D.f(0)+f(2)³2f(1) |
函数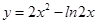 的的单调递增区间是 ( )
的的单调递增区间是 ( )
A.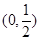 | B.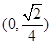 |
C.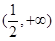 | D.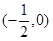 和 和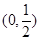 |
已知函数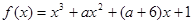 有极大值和极小值,则实数
有极大值和极小值,则实数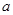 的取值范围是
的取值范围是
A.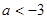 或 或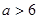 | B.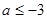 或 或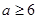 |
C.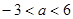 | D.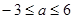 |
求曲线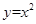 与
与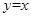 所围成图象的面积,其中正确的是( )
所围成图象的面积,其中正确的是( )
A.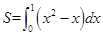 | B.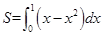 |
C.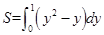 | D.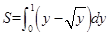 |
如图,是函数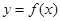 的导函数
的导函数 的图象,则下面判断正确的是
的图象,则下面判断正确的是
A.在区间(-2,1)上 是增函数; 是增函数; |
B.在区间(1,2)上 是减函数; 是减函数; |
C. 有一个极大值,两个极小值; 有一个极大值,两个极小值; |
D.当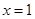 时, 时, 取极大值, 取极大值,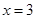 , , 取极小值. 取极小值. |
函数 的定义域为
的定义域为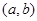 ,其导函数
,其导函数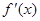 在
在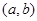 内的图象如图所示,则函数
内的图象如图所示,则函数 在区间
在区间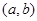 内极大值点的个数是( )
内极大值点的个数是( )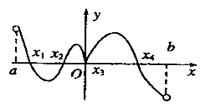
| A.1 | B.2 | C.3 | D.4 |