题目内容
函数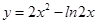 的的单调递增区间是 ( )
的的单调递增区间是 ( )
A.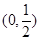 | B.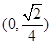 |
C.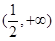 | D.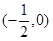 和 和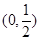 |
C
解析试题分析:求出f(x)的导函数,令导函数大于0列出关于x的不等式,求出不等式的解集即可得到x的范围即为函数的单调递增区间.对于函数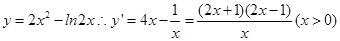 ,可知当y’>0,可知得到
,可知当y’>0,可知得到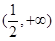 函数递增,故答案为C.
函数递增,故答案为C.
考点:导数的运用
点评:本题主要考查学生会利用导函数的正负得到函数的单调区间,同时考查了导数的计算,是一道基础题.

练习册系列答案
相关题目
函数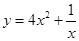 的单调递增区间为( )
的单调递增区间为( )
A.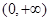 | B. | C. | D.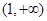 |
由抛物线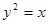 和直线x=2所围成的图形的面积等于( )
和直线x=2所围成的图形的面积等于( )
A.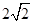 | B.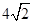 | C.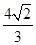 | D.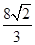 |
定义在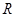 上的可导函数
上的可导函数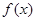 ,当
,当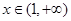 时,
时,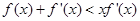 恒成立,
恒成立,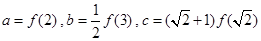 ,则
,则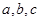 的大小关系为 ( )
的大小关系为 ( )
A.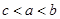 | B.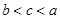 | C.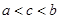 | D. |
已知定义域为R的函数 满足:
满足: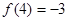 ,且对任意
,且对任意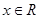 总有
总有 <3,则不等式
<3,则不等式 的解集为( )
的解集为( )
A.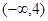 | B. | C. | D. |
已知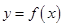 是定义在
是定义在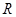 上的奇函数,且当x<0时不等式
上的奇函数,且当x<0时不等式 成立,若
成立,若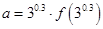 ,
, 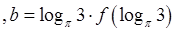
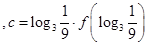 ,则
,则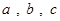 大小关系是
大小关系是
A.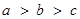 | B.c > b > a | C.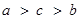 | D.c > a >b |
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( ).
| A.-1<a<2 | B.-3<a<6 |
| C.a<-1或a>2 | D.a<-3或a>6 |
函数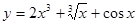 ,则导数
,则导数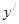 =( )
=( )
A.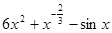 | B. |
C.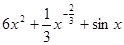 | D. |
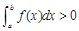 ,则f(x)>0; ⑵
,则f(x)>0; ⑵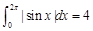 ;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则
;⑶f(x)的原函数为F(x),且F(x)是以T为周期的函数,则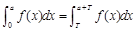 ;其中正确命题的个数为( )
;其中正确命题的个数为( )