题目内容
10.7人站成两排队列,前排3人,后排4人,现将甲、乙、丙三人加入队列,前排加一人,后排加两人,其他人保持相对位置不变,则不同的加入方法种数为( )| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
分析 分三步,第一步,从甲、乙、丙三人选一个加到前排,第二步,前排3人形成了4个空,任选一个空加一人,有4种,第三步,后排4分人,形成了5个空,任选一个空加一人,有5种,此时形成了6个空,任选一个空加一人,根据分步计数原理可得.
解答 解:第一步,从甲、乙、丙三人选一个加到前排,有3种,
第二步,前排3人形成了4个空,任选一个空加一人,有4种,
第三步,后排4分人,形成了5个空,任选一个空加一人,有5种,此时形成了6个空,任选一个空加一人,有6种,
根据分步计数原理可得3×4×5×6=360,
故选:C.
点评 本题考查了分步计数原理,关键是分步,属于基础题.

练习册系列答案
相关题目
12.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象过点P($\frac{π}{12}$,0),图象上与点P最近的一个最高点是Q($\frac{π}{3}$,5),则函数f(x)的一个单调递增区间为( )
| A. | [-$\frac{π}{3}$,$\frac{π}{3}$] | B. | [-$\frac{π}{4}$,$\frac{π}{2}$] | C. | [-$\frac{π}{3}$,$\frac{π}{6}$] | D. | [0,$\frac{π}{3}$] |
2.设函数y=f(x)是定义在R上的偶函数,对任意的x∈R都有f(x+6)=f(x)+f(3),则满足上述条件的f(x)可以是( )
| A. | f(x)=cos$\frac{πx}{3}$ | B. | $f(x)=sin\frac{πx}{3}$ | C. | f(x)=2cos2$\frac{πx}{6}$ | D. | f(x)=2cos2$\frac{πx}{12}$ |
19.模拟考试后,某校对甲、乙两个班的数学考试成绩进行分析,规定:不少于120分为优秀,否则为非优秀,统计成绩后,得到如下的2×2列联表,已知在甲、乙两个班全部100人中随机抽取1人为优秀的概率为$\frac{3}{10}$.
(1)请完成上面的2×2列联表
(2)根据列联表的数据,若按97.5%的可靠性要求,能否认为“成绩与班级有关系”?
(3)在“优秀”的学生人中,用分层抽样的方法抽取6人,再平均分成两组进行深入交流,求第一组中甲班学生恰有2人的概率.
参考公式与临界表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
(2)根据列联表的数据,若按97.5%的可靠性要求,能否认为“成绩与班级有关系”?
(3)在“优秀”的学生人中,用分层抽样的方法抽取6人,再平均分成两组进行深入交流,求第一组中甲班学生恰有2人的概率.
参考公式与临界表:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
20.若执行如图的程序框图,输出S的值为-4,则判断框中应填入的条件是( )


| A. | k<14 | B. | k<15 | C. | k<16 | D. | k<17 |
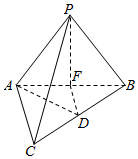 如图,在三棱锥P-ABC中,∠PAC=∠BAC=90°,PA=PB,点D,F分别为BC,AB的中点.
如图,在三棱锥P-ABC中,∠PAC=∠BAC=90°,PA=PB,点D,F分别为BC,AB的中点.