题目内容
设x和y满足不等式组
,则
的最大值 .
|
| x2+y2 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用
的几何意义求最小值.
| x2+y2 |
解答:
 解:设z=
解:设z=
,则z的几何意义为动点P(x,y)到原点距离.
作出不等式组
对应的平面区域如图:
由图象可知点A到原点的距离最大,
解得
,
及A(4,5),
所以z=
的最大值为z=
=
.
故答案为:
.
 解:设z=
解:设z=| x2+y2 |
作出不等式组
|
由图象可知点A到原点的距离最大,
|
|
及A(4,5),
所以z=
| x2+y2 |
| 42+52 |
| 41 |
故答案为:
| 41 |
点评:本题主要考查简单线性规划的应用,利用目标函数的几何意义是解决线性规划内容的基本方法,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
 把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8,则a51,25为
把正整数按上小下大、左小右大的原则排成如图三角形数表(每行比上一行多一个数):设ai,j(i、j∈N*)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a4,2=8,则a51,25为已知函数f(x)=(
)x-log2x,若实数x0是函数f(x)的零点,且0<x<x0,则函数f(x)的值( )
| 1 |
| 3 |
| A、等于0 | B、恒为正 |
| C、恒为负 | D、不大于0 |
执行如图所示的程序框图,若输出的k=6,则输入的整数p的最大值为( )
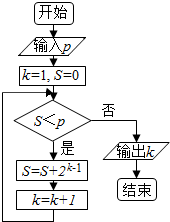

| A、7 | B、15 | C、31 | D、63 |
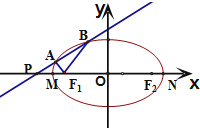 已知椭圆E:
已知椭圆E: