题目内容
若实数x,y满足不等式组
,目标函数z=x+2y,若a=1,则z的最大值为 ,若z存在最大值,则a的取值范围为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求z的最大值.若z存在最大值,利用数形结合确定满足条件的不等式关系即可.
解答:
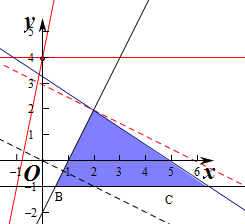
解:(1)若a=1,作出不等式组对应的平面区域如图:(阴影部分).
由z=x+2y得y=-
x+
z,
平移直线y=-
x+
z,
由图象可知当直线y=-
x+
z经过点A时,直线y=-
x+
z的截距最大,
此时z最大.
由
,解得
,即A(2,2),
代入目标函数z=x+2y得z=2×2+2=6.
(2) 由ax+y≤4,得y≤-ax+4,
由ax+y≤4,得y≤-ax+4,
则直线y=-ax+4过定点(0,4),
若-a≥0,即a≤0时,目标函数z=x+2y无最大值,此时不满足条件.
若-a<0,即a>0时,
要使z存在最大值,
则直线y=-ax+4的斜率-a,
满足-a≤-
,
即a≥
,
故此时a的取值范围为[
,+∞)
故答案为:6,[
,+∞)
由z=x+2y得y=-
| 1 |
| 2 |
| 1 |
| 2 |
平移直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
由图象可知当直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |

此时z最大.
由
|
|
代入目标函数z=x+2y得z=2×2+2=6.
(2)
 由ax+y≤4,得y≤-ax+4,
由ax+y≤4,得y≤-ax+4,则直线y=-ax+4过定点(0,4),
若-a≥0,即a≤0时,目标函数z=x+2y无最大值,此时不满足条件.
若-a<0,即a>0时,
要使z存在最大值,
则直线y=-ax+4的斜率-a,
满足-a≤-
| 1 |
| 2 |
即a≥
| 1 |
| 2 |
故此时a的取值范围为[
| 1 |
| 2 |
故答案为:6,[
| 1 |
| 2 |
点评:本题主要考查线性规划的应用,利用图象平行求得目标函数的最大值,利用数形结合是解决线性规划问题中的基本方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若a,b,c>0且a(a+b+c)+bc=4-2
,则2a+b+c的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、2
| ||
D、2
|
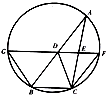 如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明: