题目内容
用单调性定义证明函数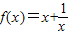 在区间[1,+∞)上是增函数.
在区间[1,+∞)上是增函数.
【答案】分析:任取区间[1,+∞)上两个实数a,b,且a<b,判断f(a)-f(b)的符号,进而得到f(a),f(b)的大小,根据单调性的定义即可得到答案.
解答:证明:任取区间[1,+∞)上两个实数a,b,且a<b
则a-b<0,ab>1,ab-1>0
则f(a)-f(b)=(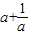 )-(
)-(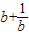 )
)
=a-b+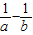 =a-b+
=a-b+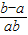
=(a-b)(1-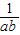 )=
)=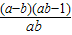 <0
<0
即f(a)<f(b)
故函数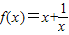 在区间[1,+∞)上是增函数
在区间[1,+∞)上是增函数
点评:本题考查的知识点是函数的单调性的判断与证明,利用定义法(作差法)证明单调性的步骤是:设元→作差→分解→断号→结论.
解答:证明:任取区间[1,+∞)上两个实数a,b,且a<b
则a-b<0,ab>1,ab-1>0
则f(a)-f(b)=(
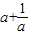 )-(
)-(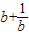 )
)=a-b+
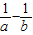 =a-b+
=a-b+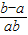
=(a-b)(1-
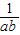 )=
)=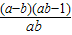 <0
<0即f(a)<f(b)
故函数
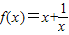 在区间[1,+∞)上是增函数
在区间[1,+∞)上是增函数点评:本题考查的知识点是函数的单调性的判断与证明,利用定义法(作差法)证明单调性的步骤是:设元→作差→分解→断号→结论.

练习册系列答案
相关题目
 设f(x)=
设f(x)=