题目内容
已知函数f(x)=
,a∈R.若对于任意的x∈N*,f(x)≥4恒成立,则a的取值范围是 .
| x2+ax+7-a |
| x+1 |
考点:函数恒成立问题
专题:综合题,函数的性质及应用
分析:将问题转化为对于任意的x∈N*,
≥4恒成立,即a(x-1)≥-x2+4x-3,分类讨论,利用函数的最值关系即可得到结论.
| x2+ax+7-a |
| x+1 |
解答:
解:∵函数f(x)=
,a∈R,对于任意的x∈N*,f(x)≥4恒成立,
∴对于任意的x∈N*,
≥4恒成立,
即x2+ax+7-a≥4(x+1)恒成立,
∴a(x-1)≥-x2+4x-3,
x=1时,a∈R;
x>1,x∈N*,则a≥-x+3,∴a≥-2+3,即a≥1.
∴a的取值范围是[1,+∞).
故答案为:[1,+∞).
| x2+ax+7-a |
| x+1 |
∴对于任意的x∈N*,
| x2+ax+7-a |
| x+1 |
即x2+ax+7-a≥4(x+1)恒成立,
∴a(x-1)≥-x2+4x-3,
x=1时,a∈R;
x>1,x∈N*,则a≥-x+3,∴a≥-2+3,即a≥1.
∴a的取值范围是[1,+∞).
故答案为:[1,+∞).
点评:本题主要考查不等式恒成立问题,将不等式恒成立转化为求函数的最值是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
若函数f(x)=2sin(
x+
)(-2<x<14)的图象与x轴交于点A,过点A的直线l与函数的图象交于B、C两点,则(
+
)•
=(其中O为坐标原点)( )
| π |
| 8 |
| π |
| 4 |
| OB |
| OC |
| OA |
| A、-32 | B、32 |
| C、-72 | D、72 |
在二面角α-l-β 的半平面α内,线段AB⊥l,垂足为B;在半平面β内,线段CD⊥l,垂足为D;M为l上任一点.若AB=2,CD=3,BD=1,则AM+CM的最小值为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
双曲线
-y2=1的焦点到渐近线的距离为( )
| x2 |
| 4 |
| A、2 | ||
B、
| ||
| C、1 | ||
| D、3 |
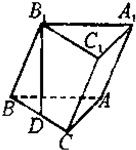 如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),点B1在底面上的射影D落在BC上.
如图,已知斜三棱柱ABC-A1B1C1的底面是直角三角形,∠C=90°,侧棱与底面所成的角为α(0°<α<90°),点B1在底面上的射影D落在BC上.