题目内容
（本小题满分10分）选修4－4：坐标系与参数方程
已知极坐标的极点在平面直角坐标系的原点
处，极轴与
轴的正半轴重合，且长度单位相同．圆
的参数方程为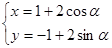
(
为参数),点
的极坐标为
. （1）化圆的参数方程为极坐标方程；
（2）若点
是圆上的任意一点, 求,两点间距离的最小值．
（Ⅰ）
（Ⅱ）
解析试题分析：（1）圆C的直角坐标方程为
，展开得
化为极坐标方程
（2）点Q的直角坐标为
，且点在圆内，由（1）知点的直角坐标为
所以
，所以
两点间距离的最小值为
考点：极坐标方程及两点间距离最值
点评：第二小题中首先求圆心到定点的距离，再利用圆的对称性求解
练习册系列答案
相关题目
（t为参数），直线l与曲线C相交于A、B两点求|AB|的值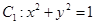
，将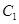
上的所有点的横坐标、纵坐标分别伸长为原来的
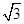、2倍后得到曲线
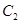. 以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线
.
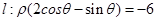的直角坐标方程和曲线
，设P、Q分别为曲线C1与曲线C2上的任意一点，求|PQ|的最小值.
中，直线l的参数方程为：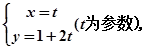
在以O为极点，以x 轴的正半轴为极轴的极坐标系中，圆C的极坐标方程为：
与圆C的位置关系.
上取两个定点
,再取两个动点 
,且
.
与
交点的轨迹
的方程；
(
)是轨迹
是轨迹
的斜率
与直线
的斜率
满足
，试探究直线
的斜率是否是定值？若是定值，求出这个定值，若不是，说明理由.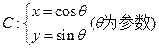
。
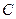的参数方程化为普通方程；
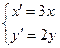后得到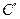曲线
，求曲线
上的动点，B为直线
的动点，求
距离的最小值。
的最大值