题目内容
在直角坐标系 上取两个定点
上取两个定点 ,再取两个动点
,再取两个动点 
 ,且
,且 .
.
(Ⅰ)求直线 与
与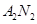 交点的轨迹
交点的轨迹 的方程;
的方程;
(Ⅱ)已知点 (
( )是轨迹
)是轨迹 上的定点,
上的定点, 是轨迹
是轨迹 上的两个动点,如果直线
上的两个动点,如果直线 的斜率
的斜率 与直线
与直线 的斜率
的斜率 满足
满足 ,试探究直线
,试探究直线 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
(Ⅰ)依题意知直线 的方程为:
的方程为: ①……………2分
①……………2分
直线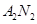 的方程为:
的方程为: ②…………………3分
②…………………3分
设 是直线
是直线 与
与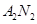 交点,①×②得
交点,①×②得
由 整理得
整理得 …………………4分
…………………4分
∵ 不与原点重合 ∴点
不与原点重合 ∴点 不在轨迹M上…………………5分
不在轨迹M上…………………5分
∴轨迹M的方程为 (
( )…………………6分
)…………………6分
(Ⅱ)∵点 (
( )在轨迹M上 ∴
)在轨迹M上 ∴ 解得
解得 ,即点A的坐标为
,即点A的坐标为
设 ,则直线AE方程为:
,则直线AE方程为: ,代入
,代入 并整理得
并整理得 …………………9分
…………………9分
设 ,
, , ∵点
, ∵点 在轨迹M上,
在轨迹M上,
∴ ③,
③,  ④………………11分
④………………11分
又 得
得 ,将③、④式中的
,将③、④式中的 代换成
代换成 ,可得
,可得 ,
, …………………………12分
…………………………12分
∴直线EF的斜率 …………………13分
…………………13分
∵
∴
即直线EF的斜率为定值,其值为
解析

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
如图所示,AC切⊙O于D,AO的延长线交⊙O于B,且AB⊥BC,若AD∶AC=1∶2,则AO∶OB=
| A.2∶1 | B.1∶1 |
| C.1∶2 | D.1∶1.5 |
 经过点
经过点 ,圆心为直线
,圆心为直线 与极轴的交点,求圆
与极轴的交点,求圆 的直线与
的直线与 轴的交点为
轴的交点为 ,与椭圆
,与椭圆  (
( 为参数)交于
为参数)交于 求
求 .
. ,过极点的直线
,过极点的直线 (
(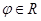 且
且 是参数)交曲线C于两点0,A,令OA的中点为M.
是参数)交曲线C于两点0,A,令OA的中点为M. 时,求M点的直角坐标.
时,求M点的直角坐标. 处,极轴与
处,极轴与 轴的正半轴重合,且长度单位相同.圆
轴的正半轴重合,且长度单位相同.圆 的参数方程为
的参数方程为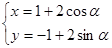 (
( 为参数),点
为参数),点 的极坐标为
的极坐标为 . (1)化圆
. (1)化圆 是圆
是圆 ,圆
,圆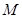 的参数方程为
的参数方程为 (其中
(其中 为参数).
为参数). 轴的正半轴重合.曲线
轴的正半轴重合.曲线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的极坐标方程是
的极坐标方程是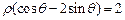 .
.
 ,
, 两点,求
两点,求 .
. 的参数方程为
的参数方程为 .以坐标原点为极点,
.以坐标原点为极点, 轴的正半轴为极轴的极坐标系中.曲线
轴的正半轴为极轴的极坐标系中.曲线 的极坐标方程为
的极坐标方程为 .
. 化成普通方程和直角坐标方程;并说明它们分别表示什么曲线.
化成普通方程和直角坐标方程;并说明它们分别表示什么曲线. ,使点
,使点