题目内容
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线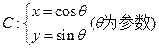 。
。
(Ⅰ)将曲线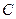 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)若把曲线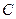 上各点的坐标经过伸缩变换
上各点的坐标经过伸缩变换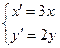 后得到曲线
后得到曲线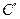 ,求曲线
,求曲线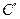 上任意一点到两坐标轴距离之积的最大值.
上任意一点到两坐标轴距离之积的最大值.
解:(Ⅰ)曲线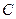 的普通方程为
的普通方程为 (3分)
(3分)
(Ⅱ)曲线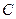 经过伸缩变换
经过伸缩变换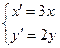 后,
后, 为参数),
为参数), ,当
,当 时取得“=”。
时取得“=”。
∴曲线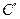 上任意一点到两坐标轴距离之积的最大值为3. (10分)
上任意一点到两坐标轴距离之积的最大值为3. (10分)
解析

练习册系列答案
相关题目
如图所示,在正三角形ABC中,D,E分别在AC,AB上,且 =
= ,AE=BE,则有
,AE=BE,则有
| A.△AED∽△BED |
| B.△AED∽△CBD |
| C.△AED∽△ABD |
| D.△BAD∽△BCD |
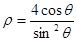 ,直线
,直线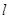 的参数方程为
的参数方程为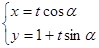 (t为参数,0≤
(t为参数,0≤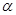 <
<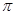 ).
).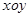 中,曲线
中,曲线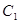 的参数方程为
的参数方程为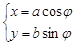 (
(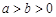 ,
,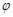 为参数),在以
为参数),在以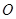 为极点,
为极点, 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线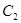 是圆心在极轴上,且经过极点的圆.已知曲线
是圆心在极轴上,且经过极点的圆.已知曲线 对应的参数
对应的参数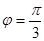 ,射线
,射线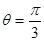 与曲线
与曲线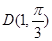 .
.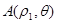 ,
,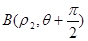 在曲线
在曲线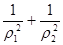 的值.
的值. 处,极轴与
处,极轴与 轴的正半轴重合,且长度单位相同.圆
轴的正半轴重合,且长度单位相同.圆 的参数方程为
的参数方程为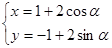 (
( 为参数),点
为参数),点 的极坐标为
的极坐标为 . (1)化圆
. (1)化圆 是圆
是圆 轴的正半轴重合.曲线
轴的正半轴重合.曲线 的极坐标方程为
的极坐标方程为 ,曲线
,曲线 的极坐标方程是
的极坐标方程是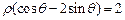 .
.
 ,
, 两点,求
两点,求 .
.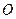 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线 的极坐标方程是
的极坐标方程是 ,直线
,直线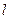 的参数方程是
的参数方程是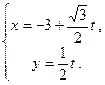 (
(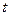 为参数)。
为参数)。 的极坐标;
的极坐标;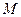 、
、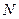 分别为曲线
分别为曲线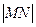 的最小值。
的最小值。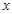 轴的正半轴为极轴建坐标系,已知曲线
轴的正半轴为极轴建坐标系,已知曲线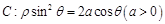 ,已知过点
,已知过点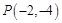 的直线
的直线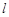 的参数方程为:
的参数方程为: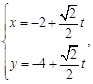 直线
直线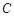 分别交于
分别交于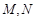
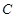 和直线
和直线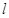 的普通方程;
的普通方程;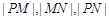 成等比数列,求
成等比数列,求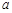 的值.
的值.  的圆心且与极轴垂直的直线的极坐标方程。
的圆心且与极轴垂直的直线的极坐标方程。