题目内容
若关于x的不等式ax2-|x+1|+2a＜0的解集为空集，则实数a的取值范围为
[
，+∞)
| ||
| 4 |
[
，+∞)
．
| ||
| 4 |
分析：先二次项系数和0的大小关系分情况讨论；再在每一种情况下找到满足要求的实数a的取值范围；最后综合即可．（注意不等式ax2-|x+1|+2a＜0的解集为空集等价于所有的函数值都大于等于0，即最小值大于等于0）．
解答：解：当a=0时，-|x+1|＜0的解集不是空集； 这种情况舍去．
又因为开口向下的二次函数图象是向下无限延伸的，
所以ax2-|x+1|+2a＜0的解集不可能为空集．这种情况舍去．
当a＞0，
当x≤-1时，不等式ax2-|x+1|+2a＜0为ax2+x+2a+1＜0
对称轴为x=
＞0，
∵关于x的不等式ax2-|x+1|+2a＜0的解集为空集，
∴f（x）min=f（-1）≥0⇒a≥0，
∴a≥0
当x＞-1时，不等式ax2-|x+1|+2a＜0为ax2-x+2a-1＜0，
对称轴为x=
＞0，
∵关于x的不等式ax2-|x+1|+2a＜0的解集为空集
∴f（x）min=f（
）≥0⇒8a2-4a-1≥0⇒a≥
，a≤
．
∴a≥
综上得：a≥
故答案为：[
，+∞）．
又因为开口向下的二次函数图象是向下无限延伸的，
所以ax2-|x+1|+2a＜0的解集不可能为空集．这种情况舍去．
当a＞0，
当x≤-1时，不等式ax2-|x+1|+2a＜0为ax2+x+2a+1＜0
对称轴为x=
| 1 |
| 2a |
∵关于x的不等式ax2-|x+1|+2a＜0的解集为空集，
∴f（x）min=f（-1）≥0⇒a≥0，
∴a≥0
当x＞-1时，不等式ax2-|x+1|+2a＜0为ax2-x+2a-1＜0，
对称轴为x=
| 1 |
| 2a |
∵关于x的不等式ax2-|x+1|+2a＜0的解集为空集
∴f（x）min=f（
| 1 |
| 2a |
| ||
| 4 |
1-
| ||
| 4 |
∴a≥
1+
| ||
| 4 |
综上得：a≥
1+
| ||
| 4 |
故答案为：[
1+
| ||
| 4 |
点评：本题考查一元二次不等式的解法，解题的关键是对参数的范围进行分类讨论，分类解不等式，此题是一元二次不等式解法中的难题，易因为分类不清与分类有遗漏导致解题失败，解答此类题时要严谨，避免考虑不完善出错．
练习册系列答案
相关题目
若关于x的不等式ax-b＞0的解集是（1，+∞），则关于x的不等式
＞0的解集是（ ）
| ax+b |
| x-2 |
| A、（-∞，-1）∪（2，+∞） |
| B、（-1，2） |
| C、（-1，2） |
| D、（-∞，1）∪（2，+∞） |
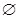，则实数a的取值范围为 ________．