题目内容
若关于x的不等式ax 2
- |x| + 2a ＜0的解集为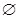
，则实数a的取值范围为 ________．
【答案】
【解析】因为关于x的不等式ax 2 - |x|
+ 2a ＜0的解集为
，则说明不等式无解，那么对于参数a讨论，只有开口向上，判别式小于等于零，可以解得实数a的取值范围为为
练习册系列答案
相关题目
若关于x的不等式ax-b＞0的解集是（1，+∞），则关于x的不等式
＞0的解集是（ ）
| ax+b |
| x-2 |
| A、（-∞，-1）∪（2，+∞） |
| B、（-1，2） |
| C、（-1，2） |
| D、（-∞，1）∪（2，+∞） |