题目内容
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为 和P,且各株大树是否成活互不影响.已知两种大树各成活1株的概率为
和P,且各株大树是否成活互不影响.已知两种大树各成活1株的概率为 .
.
(Ⅰ)求P的值;
(Ⅱ)求甲种大树成活的株数大于乙种大树成活的株数的概率;
(Ⅲ)用x,y分别表示甲、乙两种大树成活的株数,记ξ=|X-Y|,求随机变量ξ的分布列与数学期望Eξ.
解:设“甲种大树恰有i株成活”为事件Ai(i=0,1,2),则P(Ai)=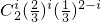 ;
;
设“乙种大树恰有i株成活”为事件Bi(i=0,1,2),则P(Bi)=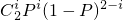 .
.
(Ⅰ)两种大树各成活1株的概率P=P(A1B1)
=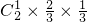 ×
×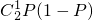 =
= ,即(2P-1)2=0,
,即(2P-1)2=0,
解得P= …(3分)
…(3分)
(Ⅱ)设“甲种大树成活的株数大于乙种大树成活的株数”为事件C,
则P(C)=P(A2B1)+P(A2B0)+P(A1B0)
=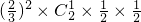 +
+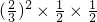 +
+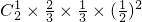 =
=
所以,甲种大树成活的株数大于乙种大树成活的株数的概率为 .…(6分)
.…(6分)
(Ⅲ)由题意知,ξ所有可能取值为0,1,2.…(7分)
P(ξ=0)=P(A2B2)+P(A1B1)+P(A0B0)
=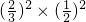 +
+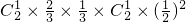 +
+ =
=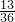 ,
,
P(ξ=2)=P(A2B0)+P(A0B2)=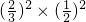 +
+ =
= ,
,
∴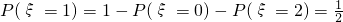
所以ξ服从的分布列为:
…(10分)
故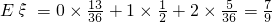 …(12分)
…(12分)
分析:设“甲种大树恰有i株成活”为事件Ai(i=0,1,2),则P(Ai)=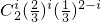 ,设“乙种大树恰有i株成活”为事件Bi(i=0,1,2),则P(Bi)=
,设“乙种大树恰有i株成活”为事件Bi(i=0,1,2),则P(Bi)=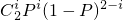 .
.
(Ⅰ)由题意可得两种大树各成活1株的概率P=P(A1B1),代入可得P的方程,解之可得;
(Ⅱ)设事件为C,则P(C)=P(A2B1)+P(A2B0)+P(A1B0),代入可得;
(Ⅲ)ξ所有可能取值为0,1,2,分别可求其概率,可得分布列,由期望的定义可得答案.
点评:本题考查离散型随机变量及其分布列,涉及数学期望的求解,属中档题.
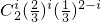 ;
;设“乙种大树恰有i株成活”为事件Bi(i=0,1,2),则P(Bi)=
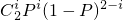 .
.(Ⅰ)两种大树各成活1株的概率P=P(A1B1)
=
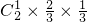 ×
×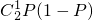 =
= ,即(2P-1)2=0,
,即(2P-1)2=0,解得P=
 …(3分)
…(3分)(Ⅱ)设“甲种大树成活的株数大于乙种大树成活的株数”为事件C,
则P(C)=P(A2B1)+P(A2B0)+P(A1B0)
=
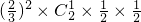 +
+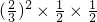 +
+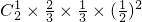 =
=
所以,甲种大树成活的株数大于乙种大树成活的株数的概率为
 .…(6分)
.…(6分)(Ⅲ)由题意知,ξ所有可能取值为0,1,2.…(7分)
P(ξ=0)=P(A2B2)+P(A1B1)+P(A0B0)
=
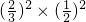 +
+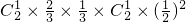 +
+ =
=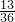 ,
,P(ξ=2)=P(A2B0)+P(A0B2)=
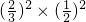 +
+ =
= ,
,∴
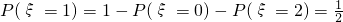
所以ξ服从的分布列为:
| ξ | 0 | 1 | 2 |
| P | 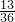 |  |  |
故
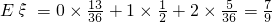 …(12分)
…(12分)分析:设“甲种大树恰有i株成活”为事件Ai(i=0,1,2),则P(Ai)=
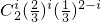 ,设“乙种大树恰有i株成活”为事件Bi(i=0,1,2),则P(Bi)=
,设“乙种大树恰有i株成活”为事件Bi(i=0,1,2),则P(Bi)=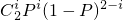 .
.(Ⅰ)由题意可得两种大树各成活1株的概率P=P(A1B1),代入可得P的方程,解之可得;
(Ⅱ)设事件为C,则P(C)=P(A2B1)+P(A2B0)+P(A1B0),代入可得;
(Ⅲ)ξ所有可能取值为0,1,2,分别可求其概率,可得分布列,由期望的定义可得答案.
点评:本题考查离散型随机变量及其分布列,涉及数学期望的求解,属中档题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目