题目内容
15.某公司即将推车一款新型智能手机,为了更好地对产品进行宣传,需预估市民购买该款手机是否与年龄有关,现随机抽取了50名市民进行购买意愿的问卷调查,若得分低于60分,说明购买意愿弱;若得分不低于60分,说明购买意愿强,调查结果用茎叶图表示如图所示.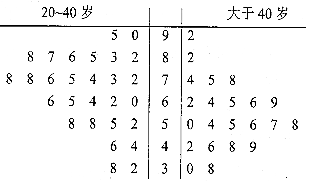
(1)根据茎叶图中的数据完成2×2列联表,并判断是否有95%的把握认为市民是否购买该款手机与年龄有关?
| 购买意愿强 | 购买意愿弱 | 合计 | |
| 20-40岁 | |||
| 大于40岁 | |||
| 合计 |
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$.
| P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 6.635 | 10.828 |
分析 (1)根据题意,填写2×2列联表,计算观测值,对照临界值表得出结论;
(2)按分层抽样方法,购买意愿弱的市民共有20人,抽样比例为$\frac{5}{20}=\frac{1}{4}$,利用列举法得出基本事件数,求出对应的概率值.
解答 解:(1)由茎叶图可得:
| 购买意愿强 | 购买意愿弱 | 合计 | |
| 20~40岁 | 20 | 8 | 28 |
| 大于40岁 | 10 | 12 | 22 |
| 合计 | 30 | 20 | 50 |
所以,没有95%的把握认为市民是否购买该款手机与年龄有关. …(6分)
(2)购买意愿弱的市民共有20人,抽样比例为$\frac{5}{20}=\frac{1}{4}$,
所以年龄在20~40岁的抽取了2人,记为a,b,
年龄大于40岁的抽取了3人,记为A,B,C,
从这5人中随机抽取2人,所有可能的情况为(a,b),(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),(A,B),(A,C),(B,C),共10种,
其中2人都是年龄大于40岁的有3种情况,所以概率为$\frac{3}{10}$. …(12分)
点评 本题考查了对立性检验与分层抽样方法和列举法求古典概型的概率问题,是综合性题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.某校有“交通志愿者”和“传统文化宣讲”两个社团,若甲、乙、丙三名学生各自随机选择参加其中一个社团,则三人不在同一个社团的概率为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{8}$ |
6.已知抛物线的焦点F到准线1的距离为p,点A与F在l的两侧,AF⊥1且AF=2p.B是抛物线上的一点.BC垂直1于点C且BC=2p.AB分别交1,CF于点D,E,则△BEF与△BDF的外接圆半径之比为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | 2 |
7.已知直线l:y=k(x-1)与抛物线C:y2=4x相交于A、B两点,过AB分别作直线x=-1的垂线,垂足分别是M、N.那么以线段MN为直径的圆与直线l的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上都有可能 |
4.函数y=sin(x+17°)-sin(x+257°)的最大值为( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |