题目内容
1.某同学参加学校自主招生3门课程的考试,假设该同学第一门课程取得优秀成绩概率为$\frac{2}{5}$,第二、第三门课程取得优秀成绩的概率分别为p,q(p<q),且不同课程是否取得优秀成绩相互独立,记ξ为该生取得优秀成绩的课程数,其分布列为| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{6}{125}$ | x | y | $\frac{24}{125}$ |
(Ⅱ)求该生取得优秀成绩课程门数的数学期望Eξ.
分析 (Ⅰ)由已知得该生至少有1门课程取得优秀成绩的对立事件是ξ=0,由此能求出该生至少有1门课程取得优秀成绩的概率,再由P(ξ=0)=$\frac{6}{125}$,P(ξ=3)=$\frac{24}{125}$,p<q,列出方程组,能求出p,q.
(Ⅱ)由已知得ξ的可能取值为0,1,2,3,分别求出相应的概率,由此能求出Eξ.
解答 解:(Ⅰ)由已知得该生至少有1门课程取得优秀成绩的概率:
P=1-P(ξ=0)=1-$\frac{6}{125}$=$\frac{119}{125}$.
∵P(ξ=0)=$\frac{6}{125}$,P(ξ=3)=$\frac{24}{125}$,p<q,
∴$\left\{\begin{array}{l}{\frac{3}{5}(1-p)(1-q)=\frac{6}{125}}\\{\frac{2}{5}pq=\frac{24}{125}}\\{p<q}\end{array}\right.$,
解得p=$\frac{3}{5}$,q=$\frac{4}{5}$.
(Ⅱ)由已知得ξ的可能取值为0,1,2,3,
P(ξ=0)=$\frac{6}{125}$,P(ξ=3)=$\frac{24}{125}$,
P(ξ=1)=$\frac{2}{5}(1-\frac{3}{5})(1-\frac{4}{5})$+$(1-\frac{2}{5})×\frac{3}{5}×(1-\frac{4}{5})$+$(1-\frac{2}{5})×(1-\frac{3}{5})×\frac{4}{5}$=$\frac{37}{125}$,
P(ξ=2)=$\frac{2}{5}×\frac{3}{5}×(1-\frac{4}{5})+\frac{2}{5}×(1-\frac{3}{5})×\frac{4}{5}$+$(1-\frac{2}{5})×\frac{3}{5}×\frac{4}{5}$=$\frac{58}{125}$,
∴Eξ=$0×\frac{6}{125}+1×\frac{37}{125}+2×\frac{58}{125}+3×\frac{24}{125}$=$\frac{9}{5}$.
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型之一.

| A. | y=-4x+3 | B. | y=-4x-3 | C. | y=4x+3 | D. | y=4x-3 |
| A. | 4x2+y2=1 | B. | x2+4y2=1 | C. | $\frac{{x}^{2}}{4}$+y2=1 | D. | x2$+\frac{{y}^{2}}{4}$=1 |
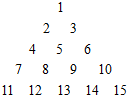 把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.
把自然数1,2,3,4,…按如图方法排成一个数阵,根据如图排列规律,求数列中第n(n≥3)行从左到右的第三个数.