题目内容
15.(Ⅰ)已知全集U={1,2,3,4,5,6,7},A={2,4,5},B={x∈U|2<x<6}.求集合B和集合(∁UA)∩B;
(Ⅱ)计算:$\sqrt{{{(π-4)}^2}}+{27^{-\;\frac{1}{3}}}-{log_2}\root{3}{2}+{(2-\sqrt{3})^0}$.
分析 (Ⅰ)根据集合的交补运算即可,
(Ⅱ)根据指数的运算性质计算即可.
解答 解:(Ⅰ)由已知得B={x∈U|2<x<6}={3,4,5},
∵全集U={1,2,3,4,5,6,7},A={2,4,5},
∴(∁UA)={1,3,6,7},
∴(∁UA)∩B={3}
(Ⅱ)$\sqrt{{{(π-4)}^2}}+{27^{-\;\frac{1}{3}}}-{log_2}\root{3}{2}+{(2-\sqrt{3})^0}$
=$|{π-4}|+\frac{1}{3}-\frac{1}{3}+1$,
=4-π+1
=5-π.
点评 本题考查了集合的混合运算和指数幂的运算性质,属于基础题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
10.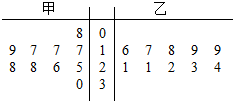 某校为了解高三学生英语听力情况,抽查了甲、乙两班各十名学生的一次英语听力成绩,并将所得数据用茎叶图表示(如图所示),则以下判断正确的是( )
某校为了解高三学生英语听力情况,抽查了甲、乙两班各十名学生的一次英语听力成绩,并将所得数据用茎叶图表示(如图所示),则以下判断正确的是( )
 某校为了解高三学生英语听力情况,抽查了甲、乙两班各十名学生的一次英语听力成绩,并将所得数据用茎叶图表示(如图所示),则以下判断正确的是( )
某校为了解高三学生英语听力情况,抽查了甲、乙两班各十名学生的一次英语听力成绩,并将所得数据用茎叶图表示(如图所示),则以下判断正确的是( )| A. | 甲组数据的众数为28 | B. | 甲组数据的中位数是22 | ||
| C. | 乙组数据的最大值为30 | D. | 乙组数据的极差为16 |
20.已知数列{an}的前n项和为${S_n}={n^2}-2n$,则a3+a17=( )
| A. | 36 | B. | 35 | C. | 34 | D. | 33 |
7.PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5得数据如下表:
(Ⅰ)根据上表数据求出y与x的线性回归直线方程$\hat y=\hat bx+\hat a$,
(Ⅱ)若周六同一时间段车流量是25万辆,试根据(Ⅰ)中求出的线性回归方程预测此时PM2.5的浓度是多少?(保留整数)
参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$:方程$\hat y=\hat bx+\hat a$.
| 时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
| 车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
| PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(Ⅱ)若周六同一时间段车流量是25万辆,试根据(Ⅰ)中求出的线性回归方程预测此时PM2.5的浓度是多少?(保留整数)
参考公式其中$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$:方程$\hat y=\hat bx+\hat a$.
 如图,茎叶图记录了某校“春季运动会”甲、乙两名运动员的成绩,他们的平均成绩均为82分,则x+y=( )
如图,茎叶图记录了某校“春季运动会”甲、乙两名运动员的成绩,他们的平均成绩均为82分,则x+y=( ) 已知斜率为1的直线l经过抛物线y2=2px(p>0)的焦点F,且与抛物线相交于A,B两点,|AB|=4.
已知斜率为1的直线l经过抛物线y2=2px(p>0)的焦点F,且与抛物线相交于A,B两点,|AB|=4.