题目内容
16．f′（x）＞0在（a，b）上成立是f（x）在（a，b）上单调递增的充分不必要条件条件．分析 在（a，b）内，f'（x）＞0，则f（x）在（a，b）内单调递增，但f（x）在（a，b）内单调递增则在（a，b）内，不能得到f'（x）＞0，如函数x3，根据必要条件、充分条件与充要条件的判断条件可得结论．
解答 解：∵在（a，b）内，f'（x）＞0，
∴f（x）在（a，b）内单调递增．
而f（x）在（a，b）内单调递增则在（a，b）内，f'（x）≥0
故答案为：充分不必要条件
点评 本题主要考查了利用导数研究函数的单调性，以及必要条件、充分条件与充要条件的判断，属于基础题．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
6．随着“全面二孩”政策推行，我市将迎来生育高峰．今年新春伊始，宜城各医院产科就已经是一片忙碌，至今热度不减．卫生部门进行调查统计，期间发现各医院的新生儿中，不少都是“二孩”；在市第一医院，共有40个猴宝宝降生，其中20个是“二孩”宝宝；市妇幼保健院共有30个猴宝宝降生，其中10个是“二孩”宝宝．
（I）从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询．
①在市第一医院出生的一孩宝宝中抽取多少个？
②若从7个宝宝中抽取两个宝宝进行体检，求这两个宝宝恰出生不同医院且均属“二孩”的概率；
（Ⅱ）根据以上数据，能否有85%的把握认为一孩或二孩宝宝的出生与医院有关？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
（I）从两个医院当前出生的所有宝宝中按分层抽样方法抽取7个宝宝做健康咨询．
①在市第一医院出生的一孩宝宝中抽取多少个？
②若从7个宝宝中抽取两个宝宝进行体检，求这两个宝宝恰出生不同医院且均属“二孩”的概率；
（Ⅱ）根据以上数据，能否有85%的把握认为一孩或二孩宝宝的出生与医院有关？
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| P（k2＞k0） | 0.4 | 0.25 | 0.15 | 0.10 |
| k0 | 0.708 | 1.323 | 2.072 | 2.706 |
7．命题?x∈R，x2-x-1＜0的否定是（ ）
| A． | ?x∈R，x2-x-1≥0 | B． | ?x∈R，x2-x-1＜0 | C． | ?x∈R，x2-x-1＞0 | D． | ?x∈R，x2-x-1≥0 |
11．某师范院校志愿者协会有10名同学，成员构成如表，其中表中部分数据不清楚，只知道从这10名同学中随机抽取一位，抽到该名同学为“中文专业”的概率为$\frac{1}{5}$．
现从这10名同学中随机选取3名同学参加社会公益活动（每位同学被选到的可能性相同）
（Ⅰ）求m，n的值；
（Ⅱ）求选出的3名同学恰为专业互不相同的概率．
（Ⅲ）设ξ为选出的3名同学中“女生”的人数，求随机变量ξ的分布列及其数学期望Eξ．
| 专业 性别 | 中文 | 英语 | 数学 | 体育 |
| 男 | m | 1 | n | 1 |
| 女 | 1 | 1 | 1 | 1 |
（Ⅰ）求m，n的值；
（Ⅱ）求选出的3名同学恰为专业互不相同的概率．
（Ⅲ）设ξ为选出的3名同学中“女生”的人数，求随机变量ξ的分布列及其数学期望Eξ．
6．
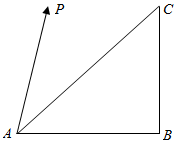等腰直角△ABC的直角顶点为B，两条直角边长都为1，点P为三角形所在平面内的一点，若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$，且|$\overrightarrow{AP}$|=1，则λ的取值范围为（ ）
等腰直角△ABC的直角顶点为B，两条直角边长都为1，点P为三角形所在平面内的一点，若$\overrightarrow{AP}$=$λ\overrightarrow{AB}$+$μ\overrightarrow{AC}$，且|$\overrightarrow{AP}$|=1，则λ的取值范围为（ ）| A． | [-1，$\sqrt{2}$] | B． | [-$\sqrt{2}$，$\sqrt{2}$] | C． | [-$\sqrt{2}$，1] | D． | [-1，1] |