题目内容
【题目】已知球
为正四面体
的外接球，
，过点
作球的截面，则截面面积的取值范围为____________________。
【答案】
【解析】
在平面中，过圆内一点的弦长何时最长，何时最短，类比在空间中，过球内一点的球的大圆面积最大，与此大圆垂直的截面小圆面积最小.利用正四面体的性质及球的性质求正四面体外接球的半径、小圆半径，确定答案.
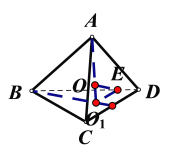
因为正四面体棱长为AB=3，所以正四面体外接球半径R=
.由球的性质，当过E及球心O时的截面为球的大圆，面积最大，最大面积为
；当过E的截面与EO垂直时面积最小，取△BCD的中心
，因为
为正四面体，所以
平面BCD ,O在
上，
，所以
,
在三角形
中，由
,
，
,
，
由余弦定理
在直角三角形
中
所以过E且与EO垂直的截面圆的半径r为
，截面面积为
.
所以所求截面面积的范围是
.
练习册系列答案
相关题目
