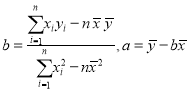题目内容
【题目】已知命题
方程
表示焦点在
轴上的椭圆，命题
双曲线
的离心率
，若“
”为假命题，“
”为真命题，则
的取值范围是__________．
【答案】
【解析】分析：根据椭圆的性质，可求出命题
方程
表示焦点在
轴上的椭圆为真命题时，实数
的取值范围；根据双曲线的性质，可得命题
双曲线
的离心率
为真命题时，实数的取值范围；进而结合“
”为假命题，“
”为真命题即命题
中有且只有一个为真命题，得到答案．
详解：若命题方程表示焦点在轴上的椭圆为真命题时；
则
解得
，
则命题
为假命题时，
或
，
若命题双曲线的离心率为真命题时；
则
即
即
则命题
为假命题时，
，或
，
∵“”为假命题，“”为真命题，一次命题中有且只有一个为真命题，
当真假时，0
，
当假真时，
，
综上所述，实数的取值范围是：，或．
故答案为：
.
【题目】某种农作物可以生长在滩涂和盐碱地，它的灌溉是将海水稀释后进行灌溉.某实验基地为了研究海水浓度
对亩产量
(吨)的影响,通过在试验田的种植实验,测得了该农作物的亩产量与海水浓度的数据如下表：
海水浓度 |
|
|
|
|
|
亩产量 |
|
|
|
|
|
残差 |
|
|
|
|
|
绘制散点图发现,可以用线性回归模型拟合亩产量(吨)与海水浓度之间的相关关系，用最小二乘法计算得与
之间的线性回归方程为
.
（1）求
的值；
（2）统计学中常用相关指数
来刻画回归效果，越大，回归效果越好，如假设
，就说明预报变量的差异有
是解释变量引起的.请计算相关指数(精确到
),并指出亩产量的变化多大程度上是由浇灌海水浓度引起的？
（附：残差
，相关指数
，其中
）
【题目】随着共享单车的蓬勃发展，越来越多的人将共享单车作为短距离出行的交通工具.为了解不同年龄的人们骑乘单车的情况，某共享单车公司对某区域不同年龄的骑乘者进行了调查，得到数据如下：
年龄 | 15 | 25 | 35 | 45 | 55 | 65 |
骑乘人数 | 95 | 80 | 65 | 40 | 35 | 15 |
（1）求
关于
的线性回归方程，并估计年龄为40岁人群的骑乘人数；
（2）为了回馈广大骑乘者，该公司在五一当天通过
向每位骑乘者的前两次骑乘分别随机派送一张面额为1元，或2元，或3元的骑行券.已知骑行一次获得1元券，2元券，3元券的概率分别是
，
，
，且每次获得骑行券的面额相互独立.若一名骑乘者五一当天使用了两次该公司的共享单车，记该骑乘者当天获得的骑行券面额之和为
，求的分布列和数学期望.
参考公式：
，
.
参考数据：
，
.
【题目】某生产企业研发了一种新产品，该产品在试销一个阶段后得到销售单价
（单位：元）和销售量
（单位：万件）之间的一组数据，如下表所示：
销售单价 |
|
|
|
|
|
销售量 |
|
|
|
|
|
（1）根据表中数据，建立关于的线性回归方程；
（2）从反馈的信息来看，消费者对该产品的心理价（单位：元/件）在
内，已知该产品的成本是
元，那么在消费者对该产品的心理价的范围内，销售单价定为多少时，企业才能获得最大利润？（注：利润=销售收入-成本）
参考数据：
参考公式：
