Question

【题目】已知四棱锥中，平面，，，，是线段的中点。

（1）求证：平面；

（2）试在线段上确定一点，使得平面，并加以证明。

Answer 1

【答案】（1）见解析（2）存在线段上的中点，使平面，详见解析

【解析】

（1）利用条件判断CM与PA、AB垂直，由直线与平面垂直的判定定理可证.

（2）取PB的中点Q，PA的中点F，判断四边形CQFD为平行四边形，利用直线与平面平行的判定定理可证；或取PB中点Q，证明平面CQM与平面DAP平行，再利用两平面平行的性质可证.

解：（1）∵，∴是等边三角形，

∴，

又∵平面，平面，

∴，

又∵，

∴平面；

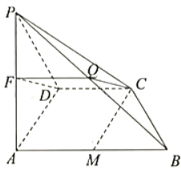
（2）取线段的中点，线段的中点，连结，

∴，

∵是线段的中点，，

∴，∴是平行四边形，

∴，

又∵平面，平面，

∴平面，

即存在线段上的中点，使平面.