题目内容
已知点O为△ABC内一点，且
+2
+3
=
，则△AOB、△AOC、△BOC的面积之比等于 ．
| OA |
| OB |
| OC |
| 0 |
考点：向量数乘的运算及其几何意义
专题：平面向量及应用
分析：根据题意，作出图形，利用向量的关系，求出△AOB、△AOC、△BOC与△ABC的面积关系，即可得出它们的面积之比是多少．
解答：
解：如图所示，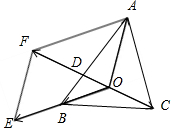
延长OB到点E，使得
=2
，分别以
，
为邻边作平行四边形OAFE；
则
+2
=
+
=
，
∵
+2
+3
=
，∴-
=3
，
又∵
=
=2
，∴
=2
，
∴
=
，
∴S△ABC=2S△AOB；
同理：S△ABC=3S△AOC，S△ABC=6S△BOC；
∴△AOB，△AOC，△BOC的面积比=3：2：1．
故答案为：3：2：1．
延长OB到点E，使得
| OE |
| OB |
| OA |
| OE |
则
| OA |
| OB |
| OA |
| OE |
| OF |
∵
| OA |
| OB |
| OC |
| 0 |
| OF |
| OC |
又∵
| AF |
| OE |
| OB |
| DF |
| OD |
∴
| CO |
| OD |
∴S△ABC=2S△AOB；
同理：S△ABC=3S△AOC，S△ABC=6S△BOC；
∴△AOB，△AOC，△BOC的面积比=3：2：1．
故答案为：3：2：1．
点评：本题考查了平面向量的应用问题，解题的关键是作出辅助线，根据向量的知识得出各小三角形与原三角形面积之间的关系，是中档题．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
执行如图所示的程序框图，若输入n的值为8，则输出Sn=
=6n2+6n的值为（ ）
| n(12+12n) |
| 2 |
| A、4 | B、8 | C、10 | D、12 |
如图是某几何体的三视图，则该几何体的体积为（ ）
| A、π | ||
B、
| ||
C、
| ||
| D、2π |