题目内容
设全集U=[0,+∞],A={x|x2-2x-3≥0},B={x|x2+a<0},若(∁UA)∪B=∁UA,则a的取值范围是 .
考点:交、并、补集的混合运算
专题:集合
分析:求出集合A,B的等价条件,利用集合关系即可得到结论.
解答:
解:A={x|x2-2x-3≥0}={x|x≥3或x≤-1},B={x|x2<-a},
则∁UA={x|0≤x<3},
若(∁UA)∪B=∁UA,则B⊆∁UA,
若a≥0,则B=∅,满足条件B⊆∁UA.
若a<0,此时B={x|0≤x<
},满足
≤3,
解得-3≤a<0,
综上a≥-3,
故答案为:[-3,+∞)
则∁UA={x|0≤x<3},
若(∁UA)∪B=∁UA,则B⊆∁UA,
若a≥0,则B=∅,满足条件B⊆∁UA.
若a<0,此时B={x|0≤x<
| -a |
| -a |
解得-3≤a<0,
综上a≥-3,
故答案为:[-3,+∞)
点评:本题主要考查集合的基本运算和集合的关系的应用,要求熟练掌握集合的交并补运算,比较基础.

练习册系列答案
相关题目
设函数f(x)在区间(-3,4)内为增函数,则( )
| A、f(-1)>f(1) |
| B、f(-1)=f(1) |
| C、f(-1)<f(1) |
| D、以上都有可能 |
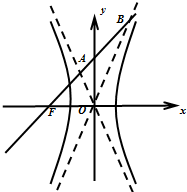 如图所示,已知双曲线
如图所示,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2
|
函数f(x)=lnx-
的零点所在的大致区间是( )
| 2 |
| x |
| A、(1,2) | ||
| B、(2,3) | ||
C、(1,
| ||
| D、(e,+∞) |