题目内容
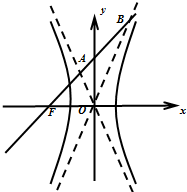 如图所示,已知双曲线
如图所示,已知双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、2
|
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:设左焦点为(-c,0),直线AB:y=x+c,求出双曲线的渐近线方程,联立直线方程求得交点A,B的坐标,再由
|OB|=2|OA|,运用两点的距离公式,结合离心率公式计算即可得到,注意a<b.
|OB|=2|OA|,运用两点的距离公式,结合离心率公式计算即可得到,注意a<b.
解答:
解:设左焦点为(-c,0),直线AB:y=x+c,
双曲线
-
=1(a>0,b>0)的渐近线方程为y=±
x,
由直线AB和渐近线方程可得交点A(
,
),B(
,
)(a<b),
由|OB|=2|OA|,可得|OB|2=4|OA|2,
即有(
)2+(
)2=4[(
)2+(
)2],
化简得4(b-a)2=(b+a)2,
即有3a2-10ab+3b2=0,
即有a=3b(舍去)或b=3a,
则c=
=
a,
e=
=
.
故选B.
双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
由直线AB和渐近线方程可得交点A(
| ac |
| -b-a |
| bc |
| b+a |
| ac |
| b-a |
| bc |
| b-a |
由|OB|=2|OA|,可得|OB|2=4|OA|2,
即有(
| ac |
| b-a |
| bc |
| b-a |
| ac |
| -b-a |
| bc |
| b+a |
化简得4(b-a)2=(b+a)2,
即有3a2-10ab+3b2=0,
即有a=3b(舍去)或b=3a,
则c=
| a2+b2 |
| 10 |
e=
| c |
| a |
| 10 |
故选B.
点评:本题考查双曲线的方程和性质,考查离心率的求法,考查两直线的交点问题,考查运算能力,属于基础题和易错题.

练习册系列答案
相关题目
集合A={(x,y)|函数y=f(x),x∈(0,1)},B={(x,y)|x=a,a∈R,a是常数},则A∩B中元素个数是( )
| A、至少有1个 |
| B、有且只有1个 |
| C、可能2个 |
| D、至多有1个 |
经过棱锥的高的两个三等分点作两个平行于棱锥底面的截面,则这个棱锥被这两个截面分成的三部分的体积比为( )
| A、1:2:3 |
| B、4:9:27 |
| C、1:8:27 |
| D、1:7:19 |
已知双曲线
-
=1的右焦点坐标为(
,0),则该双曲线的渐近线方程为( )
| x2 |
| 9 |
| y2 |
| b2 |
| 13 |
A、±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
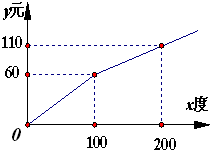 某地的水电资源丰富,并且得到了较好的开发,电力充足.某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的关系如图所示.
某地的水电资源丰富,并且得到了较好的开发,电力充足.某供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的关系如图所示.