题目内容
【题目】在四棱锥P﹣ABCD中，底面是边长为2的菱形，∠BAD=60°，PB=PD=2，AC∩BD=O． （Ⅰ）证明：PC⊥BD
（Ⅱ）若E是PA的中点，且△ABC与平面PAC所成的角的正切值为 
，求二面角A﹣EC﹣B的余弦值．
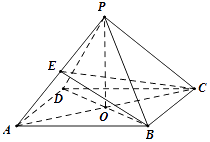
【答案】证明：（Ⅰ）因为底面是菱形，所以BD⊥AC．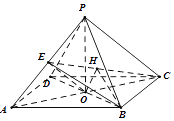 
又PB=PD，且O是BD中点，所以BD⊥PO．
PO∩AC=O，所以BD⊥面PAC．
又PC面PAC，所以BD⊥PC．
（Ⅱ）由（Ⅰ）可知，OE是BE在面PAC上的射影，
所以∠OEB是BE与面PAC所成的角．
在Rt△BOE中， 
，BO=1，所以 
．
在Rt△PEO中， 
， ，所以 
．
所以 
，又 
，
所以PO2+AO2=PA2 ， 所以PO⊥AO．
又PO⊥BD，BD∩AO=O，所以PO⊥面ABCD．
方法一：
过O做OH⊥EC于H，由（Ⅰ）知BD⊥面PAC，所以BD⊥EC，所以EC⊥面BOH，BH⊥EC，
所以∠OHB是二面角A﹣EC﹣B的平面角．
在△PAC中， 
，所以PA2+PC2=AC2 ， 即AP⊥PC．
所以 
．
，得 
， 
， 
，所以二面角A﹣EC﹣B的余弦值为 
方法二：
如图，以 
建立空间直角坐标系，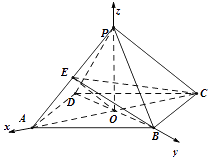
，B（0，1，0）， 
， 
， 
， 
， 
．
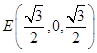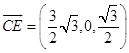设面BEC的法向量为 
，则 
，
即 
，得方程的一组解为 
，
即 
．
又面AEC的一个法向量为 
，
所以 
，所以二面角A﹣EC﹣B的余弦值为 ．
【解析】（Ⅰ）证明BD⊥AC，BD⊥PO，推出BD⊥面PAC，然后证明BD⊥PC．（Ⅱ）说明OE是BE在面PAC上的射影，∠OEB是BE与面PAC所成的角．利用Rt△BOE，在Rt△PEO中，证明PO⊥AO．推出PO⊥面ABCD． 方法一：说明∠OHB是二面角A﹣EC﹣B的平面角．通过求解三角形求解二面角A﹣EC﹣B的余弦值．方法二：以 
建立空间直角坐标系，求出平面BEC的法向量，平面AEC的一个法向量，利用空间向量的数量积求解即可．
【考点精析】根据题目的已知条件，利用直线与平面垂直的性质的相关知识可以得到问题的答案，需要掌握垂直于同一个平面的两条直线平行．
