Question

【题目】已知 ． （Ⅰ）求f（x）的最小正周期和最大值；
（Ⅱ）若 ，画出函数y=g（x）的图象，讨论y=g（x）﹣m（m∈R）的零点个数．

Answer 1

【答案】解：（Ⅰ）f（x）=2 =2sinxcosx+2sin2x=sin2x﹣cos2x+1= ∴f（x）的最小正周期T=π；
函数f（x）的最大值为： ；
（Ⅱ） ，利用“5点画法”，函数y=g（x）在区间 上列表为

x		-	-
		﹣π		0
		0	﹣1	0	1
	2	1		1		2

描点作图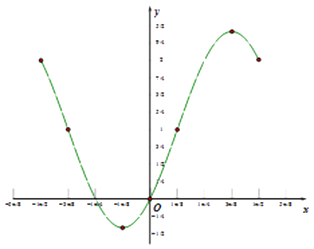

那么：y=g（x）﹣m（m∈R）的零点个数，即为函数y=g（x）与直线y=m的交点个数，
由图可知，当 时，无零点；
当 时，有1个零点；
当 或 时，有2个零点；
当m=2时，有3个零点
【解析】（Ⅰ）根据f（x）=2 ，利用向量数量积的运算法则求解f（x）并化简，即可求得f（x）的最小正周期和最大值（Ⅱ） ，利用“5点画法”画出函数y=g（x）的图象．