题目内容
设集合A={x|x2=4x},B={x|x2+2(a+1)x+a2-1=0},
(1)若A∩B=B,求a的取值范围;
(2)若A∪B=B,求a的值.
(1)若A∩B=B,求a的取值范围;
(2)若A∪B=B,求a的值.
考点:并集及其运算,交集及其运算
专题:集合
分析:(1)由A∩B=B,知B是A的子集,对集合B进行分类讨论:①若B为空集,②若B为单元集,③若B=A={4,0},由此求得a的值即可.
(2)先化简集合A,再由A∪B=B知A是B的子集,由此求得a的值.
(2)先化简集合A,再由A∪B=B知A是B的子集,由此求得a的值.
解答:
解:(1)若A∩B=B,则
①若B为空集,则△=4(a+1)2-4(a2-1)=8a+8<0
则a<-1;
②若B为单元集,则△=4(a+1)2-4(a2-1)=8a+8=0
解得:a=-1,将a=-1代入方程x2+2(a+1)x+a2-1=0得:x2=0得:x=0即B=0符合要求;
③若B=A={4,0},
即x2+2(a+1)x+a2-1=0的两根分别为4、0,
则有a2-1=0且2(a+1)=-4,
则a=1
综上所述,a≤-1或a=1.
(2)A={4,0}
∵若A∪B=B,则B?A={4,0},
∴0和4是方程x2+2(a-1)x+a2-1=0的两根
∴0+4=-2(a-1)=4
0×4=a2-1=0
解得:a=1或a=-1(舍去)
故答案为:a=1
①若B为空集,则△=4(a+1)2-4(a2-1)=8a+8<0
则a<-1;
②若B为单元集,则△=4(a+1)2-4(a2-1)=8a+8=0
解得:a=-1,将a=-1代入方程x2+2(a+1)x+a2-1=0得:x2=0得:x=0即B=0符合要求;
③若B=A={4,0},
即x2+2(a+1)x+a2-1=0的两根分别为4、0,
则有a2-1=0且2(a+1)=-4,
则a=1
综上所述,a≤-1或a=1.
(2)A={4,0}
∵若A∪B=B,则B?A={4,0},
∴0和4是方程x2+2(a-1)x+a2-1=0的两根
∴0+4=-2(a-1)=4
0×4=a2-1=0
解得:a=1或a=-1(舍去)
故答案为:a=1
点评:本小题主要考查子集与交集、并集运算的转换、一元二次方程的解等基础知识,考查分类讨论思想、方程思想.属于基础题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
设a,b为正实数,现有下列命题:
①若a2-b2=1,则a-b<1;
②若
-
=1,则a-b<1;
③若|
-
|=1,则|a-b|<1;
④若|a3-b3|=1,则|a-b|<1.
其中真命题的个数有( )
①若a2-b2=1,则a-b<1;
②若
| 1 |
| b |
| 1 |
| a |
③若|
| a |
| b |
④若|a3-b3|=1,则|a-b|<1.
其中真命题的个数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知三角形满足sinA:sinB:sinC=5:3:7,则这个三角形的最大角为( )
| A、150° | B、135° |
| C、120° | D、90° |
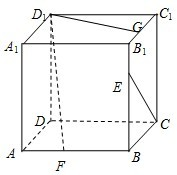 已知正方体ABCD-A1B1C1D1,点E、F、G分别是棱B1B、AB和B1C1上的动点,观察直线CE与D1F,CE与D1G.
已知正方体ABCD-A1B1C1D1,点E、F、G分别是棱B1B、AB和B1C1上的动点,观察直线CE与D1F,CE与D1G.