Question

【题目】如图，在三棱锥A﹣BCD中，已知三角形ABC和三角形DBC所在平面互相垂直，AB=BD，∠CBA=∠CBD= ，则直线AD与平面BCD所成角的大小是（ ）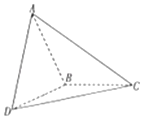
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：如图所示，过点A在平面ABC内作AO⊥BC，垂足为点O，连接OD． ∵三角形ABC和三角形DBC所在平面互相垂直，∴AO⊥平面BCD，∴AO⊥OD．
∴∠ADO是直线AD与平面BCD所成的角．
∵AB=BD，∠CBA=∠CBD= ，
∴∠ABO=∠DBO，又OB公用，
∴△OBA≌△OBD，
∴∠BOD=∠AOB= ．OA=OD．
∴∠ ．
故选：B．

【考点精析】认真审题，首先需要了解空间角的异面直线所成的角(已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则)．