Question

【题目】已知f（x）是定义在R上的奇函数，当x＞0时，f（x）= x3+ax（a∈R），且曲线f（x）在x= 处的切线与直线y=﹣ x﹣1平行．
（Ⅰ）求a的值及函数f（x）的解析式；
（Ⅱ）若函数y=f（x）﹣m在区间[﹣3， ]上有三个零点，求实数m的取值范围．

Answer 1

【答案】解：（Ⅰ）当x＞0时，f′（x）=x2+a， 因为曲线f（x）在x= 处的切线与直线y=﹣ x﹣1平行，
所以f′（ ）= +a=﹣ ，解得a=﹣1，
所以f（x）= x3﹣x，
设x＜0则f（x）=﹣f（﹣x）= x3﹣x，
又f（0）=0，所以f（x）= x3﹣x．
（Ⅱ）由（Ⅰ）知f（﹣3）=﹣6，f（﹣1）= ，f（1）=﹣ ，f（ ）=0，
所以函数y=f（x）﹣m在区间[﹣3， ]上有三个零点，
等价于函数f（x）在[﹣3， ]上的图象与y=m有三个公共点．
结合函数f（x）在区间[﹣3， ]上大致图象可知，实数m的取值范围是（﹣ ，0）．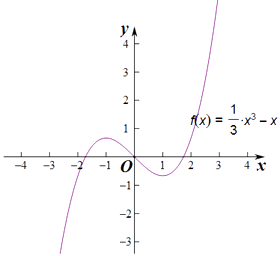

【解析】（Ⅰ）首先求得导函数，然后利用导数的几何意义结合两直线平行的关系求得a的值，由此求得函数f（x）的解析式；（Ⅱ）将问题转化为函数f（x）的图象与y=m有三个公共点，由此结合图象求得m的取值范围．
【考点精析】解答此题的关键在于理解基本求导法则的相关知识，掌握若两个函数可导，则它们和、差、积、商必可导；若两个函数均不可导，则它们的和、差、积、商不一定不可导．