题目内容
【题目】已知![]() 的三个顶点
的三个顶点![]() ,其外接圆为圆
,其外接圆为圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)对于线段![]() (包括端点)上的任意一点
(包括端点)上的任意一点![]() ,若在以
,若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,求圆
的中点,求圆![]() 的半径
的半径![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() 或
或![]() (3)
(3)![]()
【解析】
试题(1)借助题设条件直接求解;(2)借助题设待定直线的斜率,再运用直线的点斜式方程求解;(3)借助题设建立关于![]() 的不等式,运用分析推证的方法进行求解.
的不等式,运用分析推证的方法进行求解.
试题解析:
(1)![]() 的面积为2;
的面积为2;
(2)线段![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,线段
,线段![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,
,
所以![]() 外接圆圆心
外接圆圆心![]() ,半径
,半径![]() ,圆
,圆![]() 的方程为
的方程为![]() ,
,
设圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,因为直线
,因为直线![]() 被圆
被圆![]() 截得的弦长为2,所以
截得的弦长为2,所以![]() .
.
当直线![]() 垂直于
垂直于![]() 轴时,显然符合题意,即
轴时,显然符合题意,即![]() 为所求;
为所求;
当直线![]() 不垂直于
不垂直于![]() 轴时,设直线方程为
轴时,设直线方程为![]() ,则
,则![]() ,解得
,解得![]() ,
,
综上,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
(3)直线![]() 的方程为
的方程为![]() ,设
,设![]() ,
,![]() ,
,
因为点![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() ,又
,又![]() ,
,![]() 都在半径为
都在半径为![]() 的圆
的圆![]() 上,
上,
所以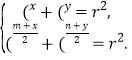 即
即![]()
因为该关于![]() ,
,![]() 的方程组有解,即以
的方程组有解,即以![]() 为圆心,
为圆心,![]() 为半径的圆与以
为半径的圆与以![]() 为圆心,
为圆心,![]() 为半径的圆有公共点,所以
为半径的圆有公共点,所以![]() ,
,
又![]() ,所以
,所以![]() 对
对![]() 成立.
成立.
而![]() 在
在![]() 上的值域为
上的值域为![]() ,所以
,所以![]() 且
且![]() .
.
又线段![]() 与圆
与圆![]() 无公共点,所以
无公共点,所以![]() 对
对![]() 成立,即
成立,即![]() .
.
故圆![]() 的半径
的半径![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目