题目内容
7.已知函数f(x)=logkx(k为常数,k>0且k≠1),且数列{f(an)}是首项为4,公差为2的等差数列.(1)求证:数列{an}是等比数列;
(2)若bn=an+f(an),当$k=\frac{1}{{\sqrt{2}}}$时,求数列{bn}的前n项和Sn的最小值;
(3)若cn=anlgan,问是否存在实数k,使得{cn}是递增数列?若存在,求出k的范围;若不存在,说明理由.
分析 (1)运用等差数列的通项公式和对数的定义,可得an=k2n+2,再由等比数列的定义即可得证;
(2)求得an,f(an),再由等差数列和等比数列的求和公式,运用单调性即可得到最小值;
(3)由题意可得(n+1)lgk<(n+2)•k2•lgk对一切n∈N*成立.讨论k>1,0<k<1,运用数列的单调性即可得到所求k的范围.
解答 解:(1)证明:由题意可得f(an)=4+2(n-1)=2n+2,
即logkan=2n+2,
∴${a_n}={k^{2n+2}}$,
∴$\frac{{{a_{n+1}}}}{a_n}=\frac{{{k^{2(n+1)+2}}}}{{{k^{2n+2}}}}={k^2}$.
∵常数k>0且k≠1,∴k2为非零常数,
∴数列{an}是以k4为首项,k2为公比的等比数列;
(2)当$k=\frac{1}{{\sqrt{2}}}$时,${a_n}=\frac{1}{{{2^{n+1}}}}$,f(an)=2n+2,
所以${S_n}=\frac{2n+2+4}{2}n+\frac{{\frac{1}{4}({1-\frac{1}{2^n}})}}{{1-\frac{1}{2}}}={n^2}+3n+\frac{1}{2}-\frac{1}{{{2^{n+1}}}}$,
因为n≥1,所以,${n^2}+3n+\frac{1}{2}-\frac{1}{{{2^{n+1}}}}$是递增数列,
因而最小值为S1=1+3+$\frac{1}{2}$-$\frac{1}{4}$=$\frac{17}{4}$.
(3)由(1)知,${c_n}={a_n}lg{a_n}=(2n+2)•{k^{2n+2}}lgk$,
要使cn<cn+1对一切n∈N*成立,
即(n+1)lgk<(n+2)•k2•lgk对一切n∈N*成立.
当k>1时,lgk>0,n+1<(n+2)k2对一切n∈N*恒成立;
当0<k<1时,lgk<0,n+1>(n+2)k2对一切n∈N*恒成立,
只需${k^2}<{({\frac{n+1}{n+2}})_{min}}$,
∵$\frac{n+1}{n+2}=1-\frac{1}{n+2}$单调递增,
∴当n=1时,${({\frac{n+1}{n+2}})_{min}}=\frac{2}{3}$.
∴${k^2}<\frac{2}{3}$,且0<k<1,∴$0<k<\frac{{\sqrt{6}}}{3}$.
综上所述,存在实数$k∈(0,\frac{{\sqrt{6}}}{3})∪(1,+∞)$满足条件.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查数列的单调性的判断和运用,以及数列不等式恒成立问题的解法,属于中档题.

| A. | 4n-1 | B. | 4n | C. | 3n | D. | 3n-1 |
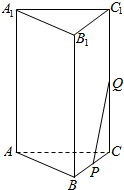 如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20.
如图,在正三棱柱ABC-A1B1C1中,已知它的底面边长为10,高为20.