题目内容
(本题满分15分)已知函数 .
.
(Ⅰ)当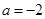 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)是否存在实数 ,使得函数
,使得函数 有唯一的极值,且极值大于
有唯一的极值,且极值大于 ?若存在,,求
?若存在,,求 的取值
的取值
范围;若不存在,说明理由;
(Ⅲ)如果对 ,总有
,总有 ,则称
,则称 是
是 的凸
的凸
函数,如果对 ,总有
,总有 ,则称
,则称 是
是 的凹函数.当
的凹函数.当 时,利用定义分析
时,利用定义分析 的凹凸性,并加以证明。
的凹凸性,并加以证明。
 .
.(Ⅰ)当
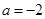 时,求函数
时,求函数 的单调区间;
的单调区间;(Ⅱ)是否存在实数
 ,使得函数
,使得函数 有唯一的极值,且极值大于
有唯一的极值,且极值大于 ?若存在,,求
?若存在,,求 的取值
的取值范围;若不存在,说明理由;
(Ⅲ)如果对
 ,总有
,总有 ,则称
,则称 是
是 的凸
的凸函数,如果对
 ,总有
,总有 ,则称
,则称 是
是 的凹函数.当
的凹函数.当 时,利用定义分析
时,利用定义分析 的凹凸性,并加以证明。
的凹凸性,并加以证明。解:(Ⅰ)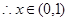 递增,
递增,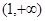 递减;
递减;
(Ⅱ)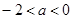 ;(Ⅲ)
;(Ⅲ)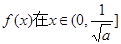 上为凸函数.
上为凸函数. 上为凹函数.
上为凹函数.
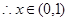 递增,
递增,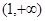 递减;
递减;(Ⅱ)
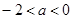 ;(Ⅲ)
;(Ⅲ)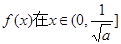 上为凸函数.
上为凸函数. 上为凹函数.
上为凹函数.本试题主要是考查了导数在研究函数中的 运用,求解函数的单调性,和函数的极值问题,以及函数的凸凹性的研究的综合运用。
(1)利用定义域和导数来求解函数的单调区间的问题。
(2)因为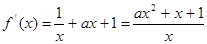
显然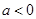 才有唯一的极值点
才有唯一的极值点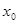 ,利用这一点得到a的不等式,从而求解范围。
,利用这一点得到a的不等式,从而求解范围。
(3)根据新的凸函数与凹函数的定义,借助于导数的思想来判定结论。
解:(Ⅰ)当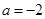 时,
时, 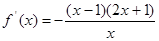 ………………2分
………………2分
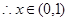 递增,
递增,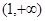 递减 ………………4分
递减 ………………4分
(Ⅱ)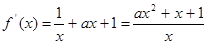
显然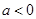 才有唯一的极值点
才有唯一的极值点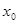 ,它满足
,它满足
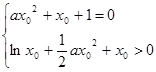 ………………6分
………………6分
消去 ,得
,得 ,
,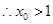
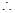 方程
方程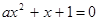 的正跟比1大
的正跟比1大
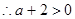 ………………8分
………………8分
故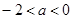 ………………9分
………………9分
(Ⅲ) 在
在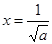 处取得最小值
处取得最小值
故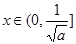 上为凸函数,
上为凸函数,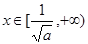 上为凹函数 ………………11分
上为凹函数 ………………11分
下证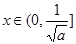 上为凸函数:
上为凸函数:
不妨设
令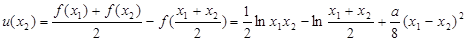 ……13分
……13分
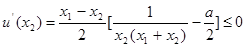
故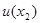 在
在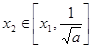 上递减,
上递减,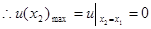

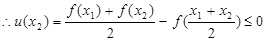
即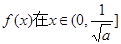 上为凸函数.
上为凸函数.
同理 上为凹函数. ………………15分
上为凹函数. ………………15分
(1)利用定义域和导数来求解函数的单调区间的问题。
(2)因为
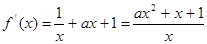
显然
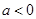 才有唯一的极值点
才有唯一的极值点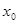 ,利用这一点得到a的不等式,从而求解范围。
,利用这一点得到a的不等式,从而求解范围。(3)根据新的凸函数与凹函数的定义,借助于导数的思想来判定结论。
解:(Ⅰ)当
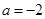 时,
时, 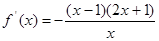 ………………2分
………………2分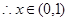 递增,
递增,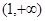 递减 ………………4分
递减 ………………4分(Ⅱ)
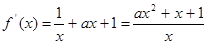
显然
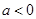 才有唯一的极值点
才有唯一的极值点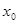 ,它满足
,它满足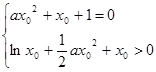 ………………6分
………………6分消去
 ,得
,得 ,
,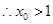
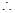 方程
方程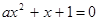 的正跟比1大
的正跟比1大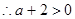 ………………8分
………………8分故
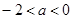 ………………9分
………………9分(Ⅲ)
 在
在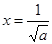 处取得最小值
处取得最小值故
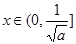 上为凸函数,
上为凸函数,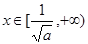 上为凹函数 ………………11分
上为凹函数 ………………11分下证
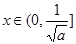 上为凸函数:
上为凸函数:不妨设

令
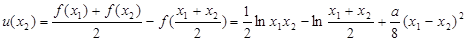 ……13分
……13分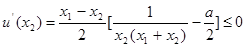
故
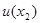 在
在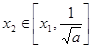 上递减,
上递减,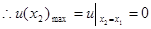

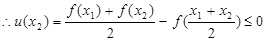
即
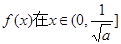 上为凸函数.
上为凸函数.同理
 上为凹函数. ………………15分
上为凹函数. ………………15分
练习册系列答案
相关题目
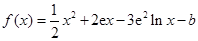 在
在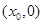 处的切线斜率为零.
处的切线斜率为零.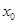 和
和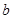 的值;
的值;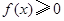 恒成立;
恒成立;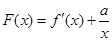 有最小值
有最小值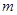 ,且
,且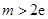 ,求实数
,求实数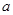 的取值范围.
的取值范围.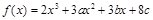 在
在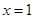 及
及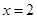 时取得极值.
时取得极值.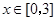 ,都有
,都有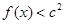 成立,求c的取值范围.
成立,求c的取值范围.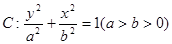 的两焦点与短轴的一个端点连结成等腰直角三角形,直线
的两焦点与短轴的一个端点连结成等腰直角三角形,直线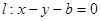 是抛物线
是抛物线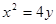 的一条切线。
的一条切线。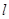 交椭圆
交椭圆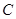 于A、B两点,若点P满足
于A、B两点,若点P满足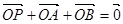 (O为坐标原点), 判断点P是否在椭圆
(O为坐标原点), 判断点P是否在椭圆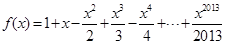 ,
,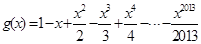 ,设函数
,设函数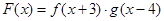 ,且函数
,且函数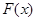 的零点均在区间
的零点均在区间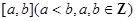 内,则
内,则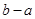 的最小值为
的最小值为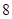
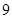
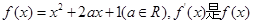 的导函数。
的导函数。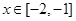 ,不等式
,不等式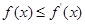 恒成立,求a的取值范围;
恒成立,求a的取值范围;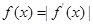 ;
;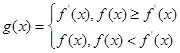 ,求
,求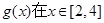 时的最小值;
时的最小值;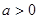 ,函数
,函数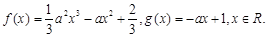
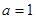 时,求函数
时,求函数 在点(1,
在点(1,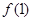 )的切线方程;
)的切线方程;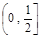 上至少存在一个实数x0,使
上至少存在一个实数x0,使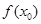 >g(xo)成立,求正实数
>g(xo)成立,求正实数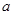 的取值范围。
的取值范围。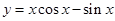 在下面哪个区间是增函数 ( )
在下面哪个区间是增函数 ( )


