题目内容
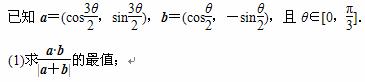 (2)是否存在k的值使|ka+b|=
(2)是否存在k的值使|ka+b|=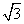 |a-kb|?
|a-kb|?
(1)由已知得
a·b=cos cos
cos -sin
-sin sin
sin =cos2θ,
=cos2θ,
 ∴y=t-
∴y=t- 为增函数,其最大值为
为增函数,其最大值为 ,最小值为-
,最小值为- ,
,
∴ 的最大值为
的最大值为 ,最小值为-
,最小值为- .
.
(2)假设存在k的值满足题设条件,则|ka+b|2=3|a-kb|2.
∵|a|=|b|=1,a·b=cos2θ,
∴cos2θ= ,
,
∵θ∈[0, ],∴-
],∴- ≤cos2θ≤1,
≤cos2θ≤1,
∴- ≤
≤ ≤1,
≤1,
∴2-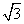 ≤k≤2+
≤k≤2+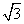 或k=-1.
或k=-1.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
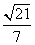 )
)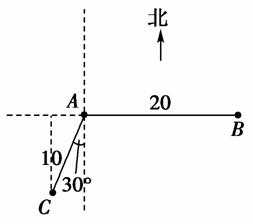


 ,则向量a与c的夹角为( )
,则向量a与c的夹角为( )
 D.
D. 
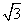 ,1),其中θ∈(0,
,1),其中θ∈(0,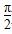 ).
). 等于( )
等于( )