题目内容
数列1,
,
,…,
的各项和为( )
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
分析:数列1,
,
,…,
一共有n+1项,然后直接利用等比数列的求和公式求解即可得到正确选项.
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
解答:解:1+
+
+…+
=
=
(1-
)
故选B.
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 3n |
1-(
| ||
1-
|
| 3 |
| 2 |
| 1 |
| 3n+1 |
故选B.
点评:本题主要考查了等比数列的求和,解题的关键弄清数列的项数,同时考查了计算能力,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案
相关题目
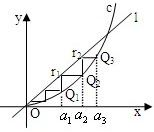 设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.