题目内容
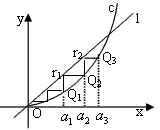
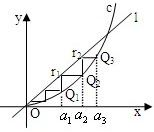 设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.(Ⅰ)试求an+1与an的关系,并求{an}的通项公式;
(Ⅱ)当a=1,a1≤
| 1 |
| 2 |
| n |
 |
| k=1 |
| 1 |
| 32 |
(Ⅲ)当a=1时,证明
| n |
 |
| k-1 |
| 1 |
| 3 |
分析:(Ⅰ)根据Qn,Pn+1,Qn+1的坐标进而求得an+1=
•
,进而通过公式法求得{an}的通项公式.
(Ⅱ)把a=1代入an+1=
•
,根据a1≤
可推断a2≤
,a3≤
,由于当k≥1时,ak+2≤a3≤
.进而可知(ak-ak+1)ak+2≤
(ak-ak+1)=
(a1-an+1)<
.
(Ⅲ)由(Ⅰ)知,当a=1时,an=
代入
(ak-ak+1)ak+2中,进而根据
(ak-ak+1)ak+2≤
(
-
)
证明原式.
| 1 |
| a |
| a | 2 n |
(Ⅱ)把a=1代入an+1=
| 1 |
| a |
| a | 2 n |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 32 |
(Ⅲ)由(Ⅰ)知,当a=1时,an=
| a | 2n-1 1 |
| n |
 |
| k-1 |
| n |
 |
| k=1 |
| 2n-1 |
 |
| i=1 |
| a | 1 i |
| a | 1 i+1 |
| a | 1 2i+2 |
解答:(Ⅰ)解:∵Qn(an-1,
),Pn+1(
•
,
),Qn+1(
•
,
).
∴an+1=
•
,
∴an=
•
=
(
•
)2=(
)1+2
=(
)1+2(
•
)22=(
)1+2+22
=(
)1+2+…+2n-2
=(
)2n-1-1
=a(
)2n-1,
∴an=a(
)2n-1.
(Ⅱ)证明:由a=1知an+1=an2,
∵a1≤
,∴a2≤
,a3≤
.
∵当k≥1时,ak+2≤a3≤
.
∴(ak-ak+1)ak+2≤
(ak-ak+1)=
(a1-an+1)<
;
(Ⅲ)证明:由(Ⅰ)知,当a=1时,an=
,
因此
(ak-ak+1)ak+2=
(
-
)
≤
(
-
)
=(1-a1)
<(1-a1)
•
=
<
.
| a | 2 n |
| 1 |
| a |
| a | 2 n |
| a | 2 n |
| 1 |
| a |
| a | 2 n |
| 1 |
| a2 |
| a | 4 n |
∴an+1=
| 1 |
| a |
| a | 2 n |
∴an=
| 1 |
| a |
| a | 2 n-1 |
| 1 |
| a |
| 1 |
| a |
| a | 2 n-2 |
| 1 |
| a |
| a | 22 n-2 |
=(
| 1 |
| a |
| 1 |
| a |
| a | 2 n-3 |
| 1 |
| a |
| a | 23 n-2 |
=(
| 1 |
| a |
| a | 2n+1 1 |
| 1 |
| a |
| a | 2n-1 1 |
| a1 |
| a |
∴an=a(
| a1 |
| a |
(Ⅱ)证明:由a=1知an+1=an2,
∵a1≤
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 16 |
∵当k≥1时,ak+2≤a3≤
| 1 |
| 16 |
∴(ak-ak+1)ak+2≤
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 32 |
(Ⅲ)证明:由(Ⅰ)知,当a=1时,an=
| a | 2n-1 1 |
因此
| n |
 |
| k=1 |
| n |
 |
| k=1 |
| a | 2k-1 1 |
| a | 2k 1 |
| a | 2k+1 1 |
| 2n-1 |
 |
| i=1 |
| a | i 1 |
| a | i+1 1 |
| a | 2i+2 1 |
=(1-a1)
| a | 2 1 |
| 2n-1 |
 |
| i=1 |
| a | 3i 1 |
| a | 2 1 |
| ||
1-
|
| ||
1+a1+
|
| 1 |
| 3 |
点评:本小题主要考查二次函数、数列、不等式等基础知识,综合运用数学知识分析问题和解决问题的能力,

练习册系列答案
相关题目
 时,证明
时,证明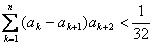 ;
;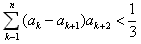 。
。
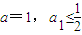 时,证明
时,证明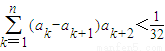 ;
;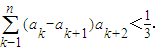 .
.